Links to tutorial material on Hubbert Linearization
Posted by Super G on July 7, 2006 - 10:06am
Some people who haven't been reading this site since the beginning might be getting a bit lost in all of the discussion of the Hubbert Linearization technique, so I thought I would post some links to some tutorial material.
According to one of the links below, the technique was introduced by Hubbert in his 1982 review paper "Techniques of Prediction as Applied to the Production of Oil and Gas", which appears in the collection Oil and Gas Supply Modeling, edited by Saul I. Gass (published as NBS Special Publication 631). I haven't found this paper on the web, but I plan to peruse the microfiche version at the library of a nearby university soon.
There is a good introduction to the technique in Kenneth Deffeyes's book Beyond Oil: The View from Hubbert's Peak.
On the web, there's a great tutorial at Wolf at the Door (which also has a lot of other tutorial material on peak oil) and there's a piece by Jean Laherrère, which is a version of a paper that appeared in Oil and Gas Journal on April 17, 2000.
Stuart introduced the technique to the TOD community here. Interestingly, it appears that Stuart actually coined the phrase "Hubbert linearization" in this post that post. (It appears in the figure titles.)
If you know of any other references or links, please leave them in the comments.

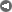


Log(P) = A + B*T + C*T^2.
The constants A, B, and C are obtained fitting. Therefore, the problem reduces to the problem of fitting a quadratic rather than a straight line. This is only slightly more difficult and can be done with spreadsheet programs like Excel. The advantage is that, unlike the Hubbard Linearization, the relationship is exact. I've done this fitting myself and it works quite well. I'll see if I can paste the chart in this post:
The problem is that:
(1) The data has noise.
(2) The correct model may not be a Gaussian.
In the U.S. case, HL may have given better early predictions of the peak than the Gaussian, but that might not be true of world data. I suppose the best we can do is to try different fitting methods and get a "rough estimate" of world peak oil production. The estimate should improve over time. As you point out in your discussion, error bars and sensitivity analysis are important.
the noise is almost always data that doesn't fit the person's pre-determined opinion from what i have seen.
The same exercise for Russia showed that post-1984 cumulative Russian production was 95% of what the HL model predicted, using only production data through 1984 to generate the predicted production profile.
I proposed the Lower 48/Russian experiment to Khebab, and he chose all of the technical parameters. If you have read any of his posts, you can tell that Khebab is an objective scientist. IMO, he is a genius.
In any case, Khebab had zero preconceived expectataions of how the results would turn out. When you look at the actual 1970 and earlier Lower 48 data and actual 1984 and earlier Russian data, they both show very strong HL patterns.
"M. King Hubbert's Lower 48 Prediction Revisited" has the HL modeling of the Lower 48.
For example, back when I was a teenager I used to grind and polish astronomical mirrors (for Newtonian and Hershel-style off-axis) reflecting telescopes. The goal was to get to the Raleigh Limit--one-eighth of a wavelength of sodium light, and the figure desired was a parablola.
Guess what: for a 4 1/4 diameter F-20 mirror I figured it to a SPHERE which is well within the Raleigh limit for a parabola, even when using the off-axis style to avoid the diffraction from a Newtonian diagonal and its support.
Even at F-12 or thereabouts for a Newtonian style, a sphere is within the Raleigh Limit for a little mirror, such as 6".
BTW, for observing planets, most nights the atmosphere is too turbulent to get much if any benefit from a telescope over 6" or 8" And on many nights a 60 mm lens on a good refractor actually shows better images than you get from a big scope because of the nature of atmospheric turbulence, which is (to put it mildly) complex.
Anyway, what matters and costs the most in amateur scopes is usually the stability of the mounting rather than the quality of the lenses and mirrors.
perhaps you understand this and you are making another point when you say Hubbert Linearization is an approximation but if so, I think you may have confused some readers that are less familiar with the subject.
At the risk of teaching the many Grannies that live here to suck eggs, Hubbert proposed that cumulative production with time (Q) followed the logistic curve (or more precisely the sigmoid curve, a special case of the logistic curve). The rate of production (P) is thus the differential of this with respect to time which gives the familiar Bell shaped curve that is like a Gaussian curve but not quite the same.
Q = Qmax/(1 + exp((th - t)k)))
P = Qmax*(t/k) * ((exp((th - t)/k)
(1-exp((th - t)/k)²))Where:-
Qmax = the ultimate cumulative production
th = the time at which half of this production is extracted
k = a constant with units of time that determines the rate of depletion, the larger k the slower the extraction.
t = time
This function gives the mathematically exact relationship
P/Q = (t/k)*(1-Q/Qmax)
This shows that were production to exactly follow Hubbert's curve a plot of P/Q against Q would give a straight line slopping down to intersect the Q axis at Qmax. The line passes thrugh Qmax/2 at th and this is the time of peak production.
Plotted the first way, the majority of the curves look like this:
_files/image006.gif)
You can see the general shape of the upside-down parabola but since it is not symmetric, it can't be the logistic curve.
Makes a nice parabola and actually this looks much better than the linearization (since it's not blowing up the misfit in the tails with a 1/Q factor). The predicted URR is within error bars of what the linearization says. I only fooled around a tiny bit, but it seems that it does ok at robust prediction too:
(BTW, as a process/communication issue I would prefer that you not accuse others of acting in bad faith ("swept under the rug"), without good evidence. It's more polite to assume that the other people simply see things differently, which is usually the case, certainly around here.)
I guess I am more into the understanding rather than the predictive properties. I just don't get how this stuff works out without any kind of forcing function included. I am categorizing this set of formulations under the heading "Immaculate Conception Hubbert Peak Analyses". Without a forcing function, I might as well look into causes of Spontaneous Human Combustion.
A thought experiment for us to engage in. Say from now out, time=T, the quantity of discoveries followed as:
K/(C + (time-T))
In this case, we would still have the peak centered at the same point but the URR will blow up to infinity. Until this is discussed by someone other than me, I can say that it is "swept under the rug", which is a mildly-offensive euphemism for "ignored". And for all I know someone has discussed this, but I don't know about it.
Oops, maybe that was an insult as well. I will try to stifle myself, and just consider anything outside the bounds of decent behavior as my attempts at snark (people such as Michael Lynch, George W. Bush, and Michael Crichton excluded).
I agree, as I've said repeatedly, that we lack a theoretical understanding of why the US production curve is so Gaussian and that's unsatisfactory. However, I view that as an interesting challenge that we should try to solve rather than a reason to dismiss the fact that it has been so up to now (modulo some noise).
It was George Stigler (I think) in his first edition (late 1940s I believe) who pointed out for the first time that BECAUSE we economists do not know the empirical shape of most supply and demand curves that we should draw them as straight lines TO EMPHASIZE THAT THEY ARE ARBITRARY AND DO NOT REFER TO THE REAL WORLD. Unfortunately, after Stigler, relatively few authors make his point, thus needlessly confusing generations of miserable and bewildered and hostile students.
HOWEVER, I shout;-)
For a small change in price for a well-behaved supply or demand function a straight line is often a pretty darn good approximation to the real world.
It is almost never a decent approximation for a large (say more than 20%) change in price.
When I taught economics I explained these nuts and bolts, and guess what: Almost half my students got a fairly good understanding of supply and demand. In the typical introductory and even intermdiate microeconomics classes at U.C., Berkeley, my guess is that fewer than ten percent grasped the most basic fundamentals of supply and demand.
Now elementary need not be hard at all. No! The problem is that most teachers of lower division classes do not give a darn about teaching and could care less that 90% of the students are ignorant of fundamentals.
Grump.
The linearization talked about here concerns a technique to turn a highly non-linear function into a straight line. It has nothing to do with small perturbations affecting linearity to the first order, as a Taylor series approximation does.
That property I do believe in but that does not influence my disagreement with the original premise of using a logistic curve or gaussian curve formulation to describe the stochastic behavior.
I think (but do not know) that Stuart agrees with my line of reasoning; he has expressed it himself in somewhat different words--just a few days ago.
The key point is that Hubbert, in 1956, accurately predicted the Lower 48 peak.
What Khebab and I attempted to address was how good the HL model was at predicting post-peak cumulative production, using only Lower 48 production data through 1970. The answer was that actual cumulative Lower 48 production was 99% of what the HL model predicted that it would be.
Assuming that Deffeyes is right that we are past the peak of conventional crude + condensate production, the HL model should therefore offer us a very accurate prediction for post-peak world production.
Projection of World Population
Where Have All the Metals Gone? (PDF)
Depletion Theory (PDF)
Crude Oil Depletion
Other papers here.
His asymmetric fit of world crude oil extraction data suggests that we are already past peak oil.
It's just another model, of course, but if the asymmetric function gives a better fit to the data over the entire data set, and it works for many different kinds of natural resource production data, then it seems to me its a very worthwhile approach.
This equation does allow asymmetrical peaks. The simplified version used by Hubbert that only allows symmetrical peaks should strictly be called the sigmoid curve although it is often referred to as the logistic curve.
I'm pretty sceptical. What it looks like to me is that the fit routine is using the asymmetry parameter to try to bend the logistic into the Gaussian tail shape of the data. It sees no cost to doing this because it's unconstrained by any post-peak data. If you look at his fit to the US data it looks more symmetric because it can't get away with that trick there to the same extent. I bet if you did a stability analysis of how the asymmety parameter varies with the length of history included, you'd find it wasn't stabilizing.
Updated Verhulst model
How can analysts throw this information away when there is a concern over too many model parameters? Having additional information does wonders for establishing a model's utility.
This is my first time on this site. I am a PhD. in Quantum Field theory who now trades shares for a living based in Hong Kong. I have almost 10 years experience in the markets. As such I feel uniquely positioned to sympathise/understand both the approaches of the people at TOD and economists who assume higher prices will stimulate exploration/production of oil.
The economists get it wrong all the time. In this case I personally believe production will be around 85mbpd depending mostly on geopolitical events over the next couple years before we enter permanent decline. Prices will soar either soon depending on geopoltical events or in any event within 5 years. The EXACT details of exactly how many bpds and in which year is largely irrelevant and can't be known now anyway as is the ultimate price of oil (it will be multiple of where we are today).
I do think that the "die-off" and other scenarios are a bit overdone and that the economists do have a point. When TSHTF (I learned that abbreviation here - thanks!) it will suit the politicians to "send out the cavalary". I think you will see MASSIVE efforts on GTL, Tar Sands, Ethanol and conservation etc. I think the economic environment will be really tough for 10 years but that we ultimately get through it. The seventies were rough but ultimately we survived.
I think the Chinese will lead the way with the alternatives. The government there doesn't have to face elections and can (and does) make tough decisions. They literally plan on the basis of ensuring commodities supplies 50 years into the future. They already have Sasol looking at GTL to produce 1mbpd. Feasilbility to take 2 years. Scale that up in the major countries and you will have enough.
I just want to say thanks for all your efforts, especially to Stuart for helping me better understand the issues.
Regards.
The impression I get from most petroleum geologists who post here is that even if spending is increased 50 fold (5,000%), output probably would not go up much or for long.
Time will tell.
Pretty soon, IMO.
If I had some money I'd stagger a few crude futures out the next few years... $70 I think may prove to be quite the good deal.
Ah, the old casino of markets...
http://futures.tradingcharts.com/marketquotes/index.php3?market=CL
Apologies for going back to an old topic. Regarding the Megaprojects I had a question. They seem to take production data and call that capacity. Is this true and if so isn't it possible that Saudi spare capacity had been eroded from 2004 to 2005, thus masking some depletion in the system? Presumably if they no longer had that spare capacity then that would effect the assumed depletion going forward - ie make it worse.
If this is the case it would be significant flaw, no?
In this and other posts there has been what I consider to be a great debate about KSA and OPEC reserves with input from mathematicians, merchant bankers (Simmons) and of course geologists (Campbell et al). I spent the weekend in the company of a senior production geologist who has worked all his life for one of the super majors and we spent a good bit of time discussing the Hubbert style approach and how it may be applied.
First point is that an oil field will only develop a bell shaped production profile if production builds with the successive drilling of production wells followed by a natural pressure decline of the reservoir. In practice this never happens as companies intervene with the natural decline process in a way that normally prioritises maximising flow rate early in field life, sometimes at the expense of lowering the ultimate recoverable reserves. Enhanced Oil Recovery (EOR) techniques commonly include water or gas injection designed to maintain reservoir pressure and sweep oil towards production wells, miscible CO2 flood and the drilling of infill wells and long reach horizontal producers which increases the contact area of the production well with the oil. Every time an intervention is excecuted the natural pressure depletion production profile gets distorted and there is a danger that any linearisation technique applied to this non- linear data will give a defective result.
Applying the Hubbert approach on a basin-wide or national scale also assumes that commercial forces have been allowed to dictate the development history in such a way that the biggest fields get found and developed first. The big fields provide infrastructure that allows for the developemnt of a large number of smaller fields. Normally there is a large degree of overlap in the development of the giants and the lesser fields and once the production for a complete basin or country is well underway then the Hubbert approach may well allow for prediction of peak production and URR for that area.
In KSA and other ME OPEC countries both of these features may be operative in opposing directions. The extensive use of water injection over the decades combined more recently with multi-lateral horizontal producers has been designed in recent years to maintain production from Ghawar, Abqaiq et al, no matter the cost. This is overalid upon historic production that has been choked back on many occasions for political reasons. The worry now is that production from the Saudi super giants may shortly collapse - giving rise to a highly irregular and assymetrical production profile for these fields - a far departure from any form of bell curve. Stuart's work in the Linearise This post of July 7th went some way towards highlighting and semi-quantifying the nature of this problem.
Western engineers who have visited KSA say that there is "bucket loads" of oil there still to be produced and this backs up to some extent what the Saudis themselves say. It seems likely that KSA and other ME OPEC countries may have a very large number of lesser undeveloped fields and in KSA these may be billion barrel+. This resouce base is not accounted for in historic production data. If work on developing these fields starts now then a production peak from these fields may be expected some time in the future - 10+ years from now? The main point is that development of this resource will come too late to delay world peak oil.
My main conclusion would be three peaks in ME OPEC production, 1974, 2006 and a third, smaller peak about 10 years from now - no mathematical basis for this but simply a geologist's gut feel.