A Dynamic Function for EROI
Posted by Rembrandt on February 29, 2012 - 3:39pm
The post below is a reproduction of a paper published in the open access journal Sustainability by Michael Dale, Susan Krumdieck, and Pat Bodger (Vol. 3). The article is a first in creating a dynamic function where Energy Return on Energy Investment changes of an energy resource are estimated over time. In this manner it becomes possible to get an estimate of how much net energy a given fossil oil, gas, coal or renewable energy source yields during its lifetime. The created EROI function is based on theoretical considerations of energy technology development and resource depletion.
Any errors in the version below the fold relative to the original are solely the responsibility of the TOD editorial team. The original version can be found via Dale M., Krumdieck S., Bodger P. A Dynamic Function for Energy Return on Investment. Sustainability. 2011; 3(10):1972-1985.
Table of contents
1. Introduction
1.1 Energy Analysis
1.2 Net Energy and EROI
2. A Dynamic Function for EROI
2.1 Theoretical considerations
2.2. Technological Component
2.3. Physical Depletion Component
2.4. Finding pmax
2.5 The EROI Function for Renewable Resources
3. Discussion
3.1 supporting evidence
3.2. What Use is the EROI Function?
4. Conclusions
References
Energy is fundamentally important to all of the processes that occur within our modern, (post)industrial society. It has been famously described by James Clerk-Maxwell as, “the ‘go’ of things” [1]. Modern society currently uses around 500 exajoules (1 EJ = 1018 J) of primary energy, 85% of which comes from fossil fuels. Some proportion of this 500 EJ must be used in the extraction and processing of energy resources, as well as in the manufacture of energy technology infrastructure, such as oil rigs and dams for hydroelectricity. This paper is intended as a discussion piece regarding some of the conceptual issues surrounding long-term dynamics of the energy supply system which maybe understood using the dynamic EROI function.
Energy analysis is the process of measuring the energy flows through the process or system under investigation. According to Boustead and Hancock [2], “Energy analysis is a technique for examining the way in which energy sources are harnessed to perform useful functions” Peet [3] classifies energy analysis as, “determination of the amount of primary energy, direct and indirect. that is dissipated in producing a good or service and delivering it to the market” reflecting the current focus of energy analyses on economic activities. Energy analysis is important for a number of reasons:
- Firstly, because of the adverse environmental impacts linked with energy transformation processes, especially of concern recently being the emission of greenhouse gases associated with the combustion of fossil fuels (possible solutions include carbon capture and storage (CCS), however the increased energy consumption entailed by CCS may (dis)favor certain methods of energy production);
- Secondly, because of the finite availability of fuels and other energy resources (whereas non-renewable resources are finite in terms of total quantity, renewable resources are finite in the magnitude of their flow) and;
- Thirdly, because of the strong link between net energy and the material standard of living and economic opportunity offered by a society [4].
There is evidence that the qualities (i.e., net energy returns) of the major energy sources in use by society (coal, oil and gas) are declining [5]. Ceteris paribus, a decline in EROI of energy resources will increase the environmental impacts of an energy production process. Also, since more energy must be extracted to deliver the same amount of net energy to society this will entail faster consumption of finite energy resources. A society dependent on energy resources with lower EROI must also commit relatively more energy to the process of harnessing energy, hence has less available for other economic activities.
Whereas standard econometric energy models, such as MESSAGE [6], MARKAL [7] and the IEA’s World Energy Model[8], account only for gross production by the energy sector, P, net energy analysis (NEA) considers all energy flows between the energy sector and the rest of the economy, as depicted in Figure 1. The energy sector receives two inputs from the rest of the economy in order to produce energy. Inputs in the form of energy, S1 enable the energy sector to run its equipment, i.e., process energy. Inputs in the form of human-made-capital (HMC), S2, are the physical plant that must be put in place in order to extract energy from the environment, e.g., oil wells, wind turbines, hydro dams, etc.
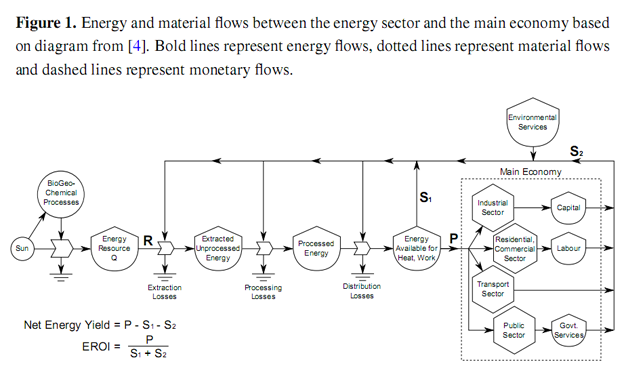
In order to determine the net energy yield or benefit (the gross energy production less energy needs for extraction and processing), P - (S1 + S2), the ratio of energy produced to the energy needed to obtain this yield, P/(S1 + S2) is known as the net energy ratio (NER) or energy-return-on-investment (EROI) [9]. A reduction in net energy yield may occur for one of three reasons:
- 1. the energy flow rate of the resource is declining, such as due to an increase in the water production of an oil field;
- 2. more energy is required to extract the resource, such as oil extraction by pumping down steam or gas during enhanced oil recovery (EOR) or;
- 3. both 1 and 2 are occurring simultaneously.
In all cases the amount of energy required to produce a unit of energy output increases. This greater energy requirement will either be made up by utilizing energy flows from within the same energy production process (internal), such as an oil producer using oil from the field to produce steam for EOR, or from energy flows originating outside of the process (external), such as an oil producer using coal or natural gas for the same purpose [10]. In the latter case, the oil production process may be competing directly with other end-uses for the energy. Many authors have begun questioning the effects that declining EROI values will have on the economy [3–5,11,12].
2. A Dynamic Function for EROI
2.1 Theoretical Considerations
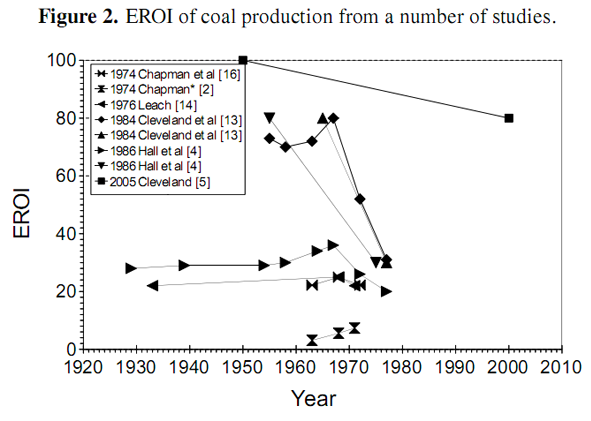
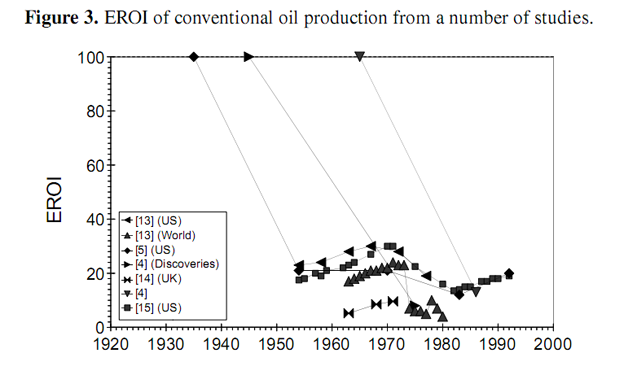
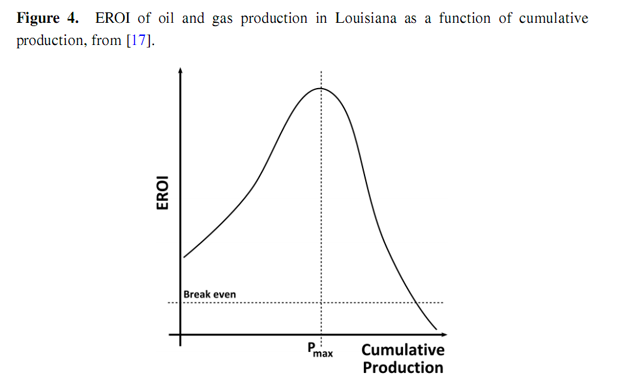
Most estimates of EROI are made as static estimates of a resource at a particular moment in time. The authors have located over 500 such estimates for all of the energy resources currently under development, as well as some still under R & D. Some dynamic estimates have been made which track the EROI of aparticular fossil resource as it changes over time. A number of such studies track the EROI of coal and oil production from various different resources over several decades [4,5,13–16], as depicted in Figures 2 and 3. The studies show that the EROI of most energy resources (coal and oil) has been either (relatively) stable at an EROI of 20–40 or decreasing over time, some from an EROI of over 100. One such study has been conducted by Costanza and Cleveland [17] of oil and gas production in Louisiana. They identify a very characteristic shape for the EROI as a function of cumulative production, as shown in Figure 4. The EROI of the resource initially increases before reaching some point of production, Pmax, at which point the energy return is at its maximum value, before declining and eventually dropping below the break-even limit represented by an EROI value of one. In this paper, we offer an explanation for the shape of this curve.
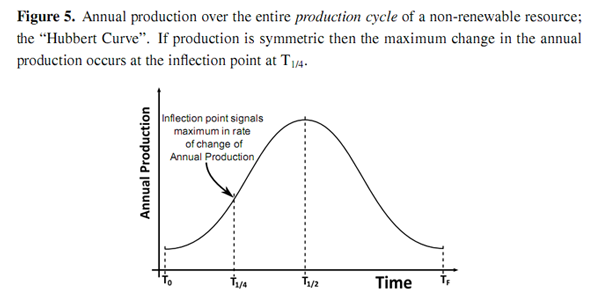
Assuming that this cycle corresponds with the production cycle identified by Hubbert for non-renewable resources [18] , at what point in the production cycle will Pmax occur? We conjecture that Pmax should occur a quarter of the way through the production cycle. Hubbert’s curve for annual production, P, as shown in Figure 5, initially increases exponentially before reaching a peak and thereafter declining. This curve passes through a point of inflection a quarter of the way through the cycle, corresponding to a maximum in the rate of change of annual production, i.e., the first derivative of annual production with respect to time, P.
The purpose of investment in increasing infrastructure is to buy an increase in annual production, therefore we may say that:

Presumably investment in infrastructure increases exponentially (or at the very minimum linearly)between T0 and T1/2. If so, then annual production and capital investment are correlated between T0 and T1/4. Thereafter, each unit of capital investment earns less return in energy production, reflected in the decreasing rate of change of energy production, P. Since EROI is the correlating factor between capital investment and energy production, then EROI must be decreasing and, hence, must have peaked before T1/4 in the production cycle. This would not be the case if investment were constant (in which case Pmax would occur when P is a maximum) or if investment were decreasing over the period. However, both of these cases seem unlikely. Within this work, we posit that this curve for the EROI is representative of not only Louisiana oil and gas but all non-renewable resources. We further assume that this EROI function is a product of two components: one technological, G, that serves to increase energy returns as a function of cumulative resource production, which serves as a proxy measure of experience, i.e., technological learning; and the other, H, diminishing energy returns due to declining physical resource quality. he function F(p) is depicted in Figure 6 along with the two components.

Where (epsilon) ε is a scaling factor that increases the EROI and p is cumulative production normalized to the size of the ultimately recoverable resource (URR). Within this work URR is assumed to be the total resource that may be recovered at positive net energy yield. In reality, epsilon and URR (or TP) would be used as parameters for scenario-based assessment or a Monte Carlo simulation. Normalised cumulative production, p is defined such that:

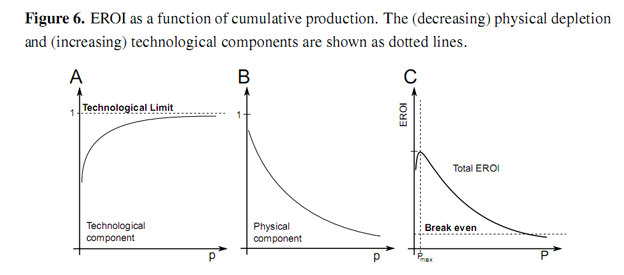
We assume that the technological component of the EROI function asymptotically increases as a function of production as shown in Figure 6. There are two factors that will influence this technological component of the EROI function: how much energy must be embodied within the equipment used to extract energy and how well that equipment performs the function of extracting energy from the nvironment. We assume that both of these factors are subject to strict physical limits. Firstly, that there is some minimum amount of energy that must be embodied in order to function as an energy extraction device, for instance the foundation of a wind turbine must successfully endure a large moment load. Secondly, there is a limit to how efficiently a device can extract energy. We further assume that, as a technology matures, i.e., as experience is gained, the processes involved become better equipped to use fewer resources: PV panels become more efficient and less energy intensive to produce; wind turbines become more efficient and increasing size allows exploitation of economies of scale. These factors serve to increase energy returns. However, it can be expected that these increases are subject to diminishing marginal returns as processes approach fundamental theoretical limits, such as the Lancaster-Betz limit in the case of wind turbines. Technological learning curves (sometimes called cost or experience curves) track the costs of production as a function of production. These often follow an exponentially declining curve asymptotically approaching some lower limit. The progress ratio specifies the production taken for costs to halve. Between 1976 and 1992, the PV module price per watt of peak power, Wp, on the world market was 82% [19]. This means that the price halved for an increase in cumulative production of 82%. Lower financial production costs should correlate with lower values of embodied energy [4,20,21]. The specific form of the function is:

where 0 < X ≤ 1.
Here X represents the initial value of the immature technology and (chi) χ represents the rate of technological learning through experience, which will be dependent on a number of both social and physical factors. This rate is assumed constant.
2.3. Physical Depletion Component
The physical resource component of the EROI function is assumed to decrease to an asymptotic limit as a function of production, as shown in Figure 6. In general, those resources that offer the best returns (whether financial or energetic) are exploited first. Attention then turns to resources offering lower returns as production continues. In general the returns offered by an energy resource will depend upon the type of source, formation and depth of the reserve, hostility of the environment, distance from demand centers and any necessary safety or environmental measures. The costs of production often increase exponentially with increases in these factors [22]. The result is that the physical component of the EROI of the resource declines as a function of production. We assume that this decline in EROI, H will follow an exponential decay:

where 0 < Φ ≤ 1.
Here (phi) Φ represents the initial value of the physical component and (lower case phi)φ represents the rate of degradation of the resource due to exploitation. Again this rate is assumed constant. We justify this exponential curve by considering the distribution of energy resources. Some of these resources will offer large energy returns due to such factors as their energy density (e.g., grades of crude or coal), their ease of accessibility (e.g., depth of oil resources, on-shore vs. offshore), their proximity to demand centers (e.g., Texan vs. Polar oil) and possible other factors. The EROI of one particular source should be, if not normal, then most likely displays a positive skew, i.e., the median is less than the mean, as depicted in Figure 7. For example, there are more sites with lower average wind speeds than with higher wind speeds.
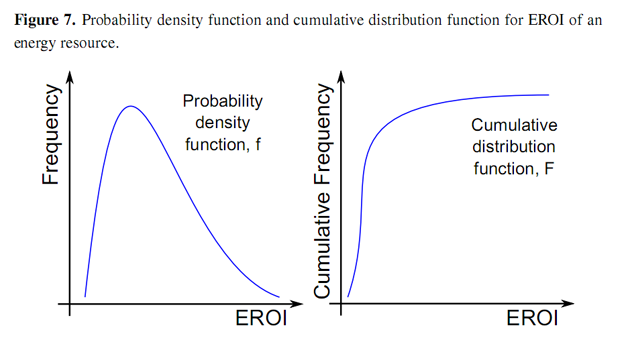
If we now assume that sites will be exploited as a function of their EROI, i.e., that those sites offering the best energy returns are exploited first, then we may now re-plot the cumulative distribution function as EROI depletion as a function of exploitation, i.e., production by rotating the axes and ranking the sites by EROI from highest to lowest.


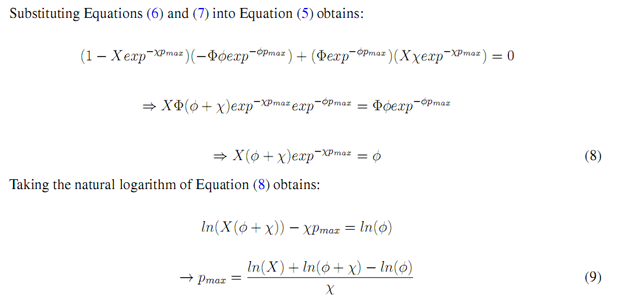
2.5. The EROI Function for Renewable Resources
Unlike non-renewable sources, for which the EROI is solely a function of cumulative production, in the case of renewable energy sources the physical component of EROI is a function of annual production. The technological component will still be a function of cumulative production, which serves as a proxy measure for experience. In this case a reduction in production means that the EROI may “move back up the slope” of this physical component. In the interim, technology, which is a function of cumulative production, will have increased, further pushing up energy returns. This entails that the EROI of a renewable energy source is a path dependent function of production. Decline in the physical component of EROI for renewable energy sources represents the likelihood of the most optimal sites being used earliest. For example, deployment of wind turbines presently occurs only in sites where the average wind speed is above some lower threshold and that are close to large demand centers to avoid the construction of large distribution networks. Over time, the availability of such optimal sites will decrease, pushing deployment into sites offering lower energy returns, which should be reflected in declining capacity factors over time.
3.1 - Supporting Evidence
We provide supporting evidence for the EROI function presented by considering wind and solar resources for the US as a case study. The technological component of the EROI may be increased by the production of wind turbines that are able to better extract energy from the passage of air. This increase is subject to an absolute physical limit represented by the Lancaster–Betz limit [23] which defines the maximum proportion of energy that may be extracted from a moving column of air as 16/27 ≅ 60%. Experience curves for wind farms show that long-term costs of energy production from wind have fallen exponentially as a function of cumulative energy production (a proxy for “experience”) [24]. The resource base for wind has been extensively (and intensively) mapped in several regions of the world. The National Renewable Energy Laboratory (NREL) Western Wind Dataset [25] was used to produce a depletion curve of the US wind resource, ranked by power density (W/m) shown in Figure 9. The power density of the wind resource initially declines exponentially as a function of land area, before dropping sharply below 500 W/m2
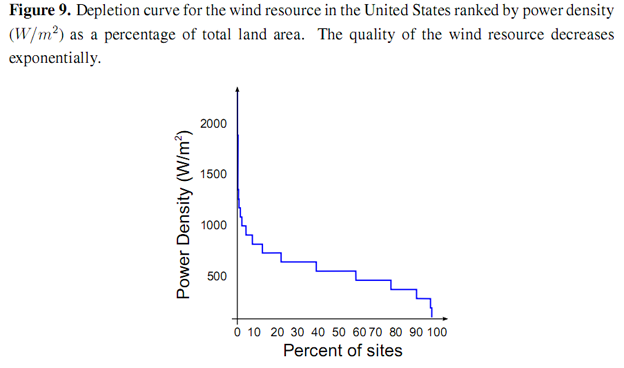
NREL have also produced the National Solar Radiation Database (NSRDB), for the mainland US [26]. This data was used to produce a depletion curve of the US solar resource ranked by energy flux density (Wh/m2/day) shown in Figure 10. The energy flux density of the solar resoure declines exponentially as a function of total land area from a maximum of just over 8,000 Wh/m2/day
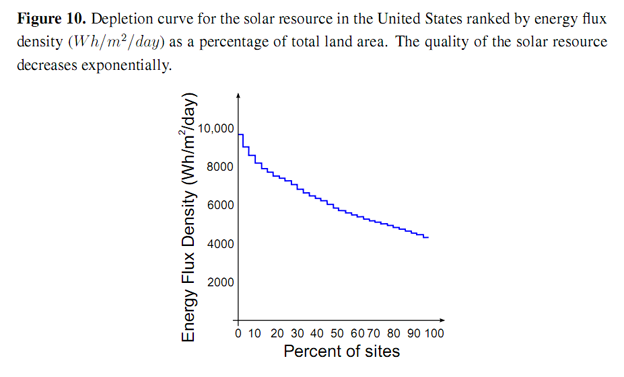
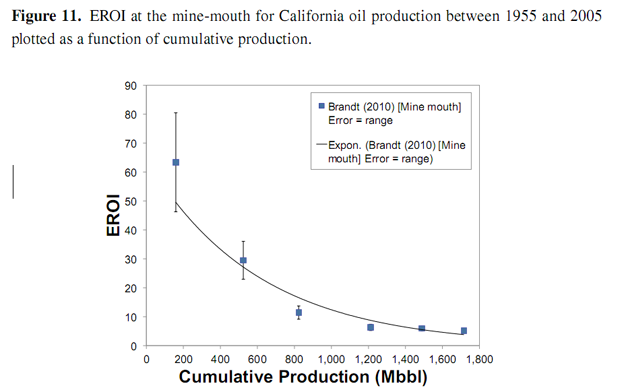
If we imagine the total resource being populated with identical turbines, each with a nominal constant embodied energy cost, (kappa) κ [GJ/MW] and a nominal lifetime tL [yr] in such a way as to exploit the best sites first, the pattern of decline of the EROI as a function of total capacity installed [MW], will follow the pattern of the power density of the sites. An analogous case may be made of the solar resource. Brandt (in press) [10] has made a long-term study of the EROI of oil production in California between 1955 and 2005. The EROI of this oil at the mine-mouth is shown in Figure 11. An exponentially decreasing curve is shown for comparison. The initial decline is greater than exponential.
3.2. What Use is the EROI Function?
Presently, long-term energy forecasting is done by predicting (or perhaps, more accurately, stipulating) long-term production costs for various energy supply and conversion technologies. This information is then used to optimize a “least-cost” energy system that meets the projected future energy demand. The problems associated with predicting something as volatile as production costs over timescales of decades is rarely discussed. The issue of declining net energy yields is never considered. EROI defines the relationship between the amount of energy that must be embodied as human-made-capital (HMC) in order to produce energy and the amount of energy that HMC can produce. In Section 1.1.1., the EROI was defined as:

Although energy dynamics are not well understood, since EROI is a physical property of an energy source, it should be easier to predict over long time periods than energy production costs (in monetary terms) or prices. The EROI function may then enable long-term energy forecasts to be made which are more accurate than those using solely price-based dynamics. Such a projection, based on the principles of energy analysis, will also automatically obey fundamental physical laws, such as the first and second laws of thermodynamics.
We have presented a top-down framework for determining the EROI of an energy source over the entire production cycle of an energy resource. This function allows production costs (in energetic terms) to be predicted into the future. This EROI function, coupled with a purely physical allocation function to allocate energy demand between different energy sources, will allow a new form of energy supply forecasting to be undertaken, based solely on physical principles.
Acknowledgements
This work would not have been possible without the support of the Department of Mechanical Engineering at the University of Canterbury and the Keith Laugesen Trust.
See the original for a full reference list.
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).



This is a very useful tool.... being able to calculate is quite valuable
[Edit - link repaired]
OK, given certain personal constraints at this moment in time (my 105 IQ, that it's near 2am in the morn - still up and about after a good win on the tennis court, perhaps a red or two coursing through my veins - my 105 IQ), I understand the dynamics of EROI. Whenever I raise the topic of oil-replacement with my fellow Joes, really there's no come-back... That cheap and positive EROI is a prerequisite for BAU is a no-brainer.
Yet, after nearly four and half years of visiting here, am I any wiser? Do I observe the PTB raise the subject in MSM? Is the future for my three fabulous kids any brighter? Not that I can see...
Where to from here? More of the same??
Cheers, Matt
Disgruntled, frustrated, concerned, fed up
Hey Joe, knowledge is power or something like that. Don't judge your kid's future happiness on whether we will have the the same energy to use or whether society has to change due to todays cheap energy sources not being around. I'm sure that the wisdom and knowledge that you have on this subject is light years ahead of the average joe, transfer that and prepare your children and they will be fine.
Setting priorities, changing expectations, and preparing for the eventual outcome might make the transition seamless to them where it won't be so seamless for people like you and me. Being first on board the Peak Oil Ark might not save the world from the great flood but at least you know whats coming so look for a silver lining when you can.
It's an inner journey for many at this point. Think of middle class reality as a game of musical chairs. At some point the chair will most likely be pulled from you and from your friends and family.
You might get a new chair but it wont be the same. The choices for this happened when I was 10 years old or so. It's nothing personal. Keep your cool and adjust according to reality.
The authors of this study have done an admirable job of presenting a complex issue in a very understandable and readable format. There is enough "meat" in terms of formulas and charts to satisfy the technically literate readers, yet the written text describes issues very clearly and can provide a basis of understanding for the non-technical readers.
Sadly, this is the type of information that should be seeping into the MSM for broader dissemination. However, for "Joe Six-Pack" and the "Drill-Baby-Drill" crowd, the message may need to conveyed by cartoons with text written at the 11th grade reading level.
OldLeatherNeck
I agree with your thought - good communication should be at a lower grade level.
But you are aiming way too high. People who teach writing suggest you should aim at 5th to 7th grade level or you will lose most of your audience. This may surprise you - but many great writers - and all marketing copywriters - aim at 5th to 7th grade in order to get their message across.
It is easy to measure your writing level - just paste it into: http://www.standards-schmandards.com/exhibits/rix/index.php
By the way - your posting is at grade level 15 (3rd year college) - far too high for the masses.
This post on EROI is at about grade level 20 - completely off the charts for most people.
Hemingway wrote at grade level 4! What I just wrote to you is level 8.
Texas-Engineer
Thanks for the comments and suggestions as well as the link to the writing level tool.
I did not realize that we needed to take messages down to that low of a level. However, after some thought I remembered that at some point this information needs to be presented to our "Congress Critters".
And in related news, "Wall Street greed fueling high gas prices"
http://www.cnn.com/2012/02/28/opinion/sanders-gas-speculation/index.html...
Bernie Sanders is probably among the *better* informed members of either house, and yet not a whisper about Peak Oil, declining exports, or rising EROEI. In all fairness, Wall Street commodities speculation does have an impact, but this is not what Joe Public really needs to hear at this point.
It's really great to have a model for EROI, and I think posts with good models is something TOD should be doing even more. For anyone who has more experience in the oil business, I wonder if the assumption that the resources with the best returns are exploited first is a valid one. Looking at the history of large discoveries, it seems that there has been a nearly uniform distribution of about one very big field per decade as seen in this graph of The Growing Gap. I suspect that discoveries might be modeled as random draws (without replacement) with some weighting towards larger fields, but maybe not too much. Once the field is discovered, there probably is a strong incentive to produce it assuming that it is expected to be economical. On the other hand, wind and solar can be exploited according to expected returns because the value of a site is quite well known before installing the equipment.
EA - Modeling isn't my strong point but the analysis seems very thorough. OTOH it's based on mathematical logic and the oil patch often doesn't follow generally acknowledged logic. Maximizing profit from the results of a drilling project isn't always the prime consideration. IMHO much of the recent shale gas boom wasn't driven so much by ROR on those drilling investments as increasing a public company's market cap by meeting Wall Street's demand for an ever increasing reserve base. Even if that increase doesn't prove to be very economical. If you missed my tale before: I once drilled 4 horizontal wells that actually lost money for the public company. The effort increased companywide production 400% but didn't add $1 of reserves that wouldn't have been produced by the existing vertical wells. The hz wells just produced the reserves much faster....at the cost of $18 million. But Wall Street didn't care: stock went from $0.75 to over $3.50 a share in just a few months. And we didn't even lie: all the details were right there in our annual report for a1nyone to read...if they bothered to. Impressed one WS raider so much his hostile takeover of the company was successful. In the effort to fight him off management raised $100 million in 11% bond money which they ultimately used most of it to pay of an 8% bank loan. Not logical? The heck is wasn't. There's a golden rule in the oil patch: screw over who ever you want but don't screw your banker. And yes...a few years later the company went bankrupt. And did the raider take a bad hit? Not too bad: he bought the 11% bonds at a 45% discount went the company faultered. He got his entire price back by delivering 100% of the companies cash flow to pay off his interest and got the $100 million write off for the bad loan. Just like making sausage: often the process isn't pretty even if the results turn out not too bad.
"I wonder if the assumption that the resources with the best returns are exploited first is a valid one". In reality we never get to choose what resources are exploited first: you exploit what you find. It might be what you drilled for but more often you find much less. Maybe nothing if it's a dry hole. Of course I would rather develop a field that generates an EROEI of 60. But that isn't what my wildcat found: I discovered a field that will generate an EROEI of 15. I'm not going to walk away from a commercial discovery. And if I'm a public company I might develop it if I only get my capex back. Bragging rights about drilling a new field discover has value to such a company even with a zero ROR. Logical? Heck yeah if you're sitting on 200,000 shares of stock options and you get to decide to develop the non-profit maker. Right now I developing a project to recover residual oil from a oil field trend in Texas that has produced over 2 billion bo. Some of these shallow fields produced over 150 million bo. But did so at a relatively slow rate and a significant operating expense. If you applied discounted cash flow economic analysis to their historical production history you would not be impressed. I can't guess the EROEI but the ROR was meager. But they were fully developed. As we say in Texas: you dance with the one what brought you. There are dozens of other scenarios I could describe. But that doesn't mean there isn't a connection between oil patch investments and EROEI. It's just a lot more complicated and won't always fit regardless how accurate that model may be on a theoretical level.
To paraphrase an old oil patch saying: you can do it fast, cheap, safe or logical...pick two.
Rockman, thanks for your answer. As you said, you dance with the one what brought you, so if you have something that produces you go ahead with it even if it isn't the best you'd hoped for. On a larger scale, the model might work because the oil is being found and developed in more remote places like moving offshore. But when Edwin Drake drilled his first well, it was in Pennsylvania and if he didn't happen to be there he could have just as easily been in Texas and maybe finding even more. Maybe the correct choice of phi in the H(p) term models this reasonably well, but it just seemed that the assumption wasn't entirely right.
EA - There's another aspect that's difficult to factor into assumptions about EROEI. Some folks have difficulty accepting current reality: oil/NG has never been easier to find then it is today. That doesn't mean there a lot to find or that we won't have to go into extreme environments to look for it. Or that it won't cost a great deal to search for and develop. But give me a 100 sq mile area in the US and if there are commercial oil/NG reserves somewhere in there I have the tools available to find it. OTOH the best 3d seismic in the world isn't going to help you if the field isn't there. The reality is that 3d seismic has prevented more wells from being drilled then it has supported. That's why the oil patch has spent many $billions for this data: to not drill dry holes as much as to find new reserves.
IMHO this is one of the biggest obstacles to estimating the significance of EROEI changing over time. About 35 years ago I was drilling 12,000' wells testing 3,000 acre POTENTIAL reservoirs. Success rate finding what I hoped to be there was maybe 20%. Today I drill 16,500' wells testing 80 acre POTENTIAL reservoirs. But with current technology my success rate can be 70% or better. Obviously the EROEI of a long ago success was much better than one of my current successes: less energy used to drill the shallower well and a lot more reserves. OTOH I also drilled a lot of wells with zero EROEI: dry holes. But an old discovery might lead to a half dozen low row risk development wells but many of my new discoveries are one well fields. A nice ROR but now I have to go find another one to test.
But how do the economics play out? There were many times in the past when discovery of a high EROEI field didn't have a great ROR due to low prices. And even during high price periods the industry's overall EROEI was pathetic. Back in the boom of the late 70's we had over 4,600 rigs drilling compared to the current 2,100 or so. That boom did lead to some reserve additions but compared to the energy/capex spent it wasn't even close to being worth the effort. Many thousands of dry holes were drilled for targets with very little chance of success. High prices and ridiculous greed feed speculation that did tremendous harm to the oil patch. Have you ever heard of the Seven Sisters? Count how many Sisters still exist today. The 70's boom is one of the prime reasons the number is less than 7 today.
And today we may be seeing the beginning of another melt down. Suddenly there are more stories about the public shale gas players cutting back on their drilling programs. Even with the pressure to satisfy Wall Street with reserve additions the ROR of many of those plays may be just to low today. But the EROEI of those plays haven't decreased significantly. Thus a project with an EROEI of 8 that might have been drilled 2 years ago won't get drilled this year. I drill conventional NG plays with much better ROR/EROEI than the shale plays. But there aren't nearly as many of them left as shale prospects. But I have to cut this year's drilling budget due to low NG prices. And just like the shale gas wells, the EROEI of my wells hasn't decreased. Doesn't matter...many aren't gonna get drilled.
And that's why, as interesting this analysis of EROEI may be, using it as a predictive tools has a good bit of uncertainty IMHO.
Count how many Sisters still exist today
The original Seven Sisters of oil who used to control 85% of world oil production:
1. Standard Oil of New Jersey (Esso)
2. Standard Oil Company of New York (Socony)
3. Standard Oil of California (Socal)
4. Texaco
5. Gulf Oil
6. Anglo-Persian Oil Company
7. Royal Dutch Shell
The remaining Seven Sisters, who now produce 10 per cent of the world’s oil and gas and hold just 3 per cent of reserves:
1. ExxonMobile (originally Esso, Socony)
2. Chevron (originally Socal, Texaco, Gulf)
3. BP (originally Anglo-Persian)
4. Royal Dutch Shell
The new Seven Sisters, who now control 1/3 of the world's oil and gas production and reserves:
1. Saudi Aramco
2. Gazprom (Russia),
3. CNPC (China)
4. NIOC (Iran)
5. PDVSA (Venezuela)
6. Petrobras (Brazil)
7. Petronas (Malaysia)
We need Mobjectivist & the oil conundrum.....
Rgds
WeekendPeak
I think Rembrandt is approaching this from the right angle.
The PDF view is useful as it puts the resource pyramid into a mathematical foundation. The tail of high EROEI gets eaten away at first and we are gradually left with that bulk of low EROEI resources.
So yes indeed, the best way to apply this is through the use of conditional/marginal probabilities. That's how one can use the dynamically changing PDF curve to ride the efficiency curve down into the ground. It's very doable, but as usual the hard part is in convincing others that the baseline data is accurate.
In mathematical terms, it works like this:
where p(g) is the grade prior and the p(E|g) is dynamically changing conditional PDF for EROEI, and out pops the efficiency. I think it is a pretty useful metric for policy discussion.
These findings contradict the belief of some that renewable energy can grow indefinitely in a positive feedback process
http://www.renewableenergyworld.com/rea/blog/post/2010/12/moores-law-of-...
I wonder if it is possible to derive the Hubbert bell curve on physical principles rather than empirically. If I understand correctly others have said the bell curve is the aggregate of lots of smaller curves some of which might be lopsided curves or even triangles. Perhaps calculus can generate the bell curve for the general case.
This could a step towards working out optimum population. We could say the world will be powered by wind, solar and geothermal and the average output will be x kilowatts per person. Optimum population will be the peak for the combined system divided by x.
A thought experiment. For the next 40 years, let's say that renewables grow at 10%/year, appliance efficiency (cars, refrigerators etc) improves at 3%/year and fossil fuels availability decreases at 2%/year. And population increases at x%/year to 9B in that time frame. Would make for an interesting graph :)
To illustrate what I mean by deriving the bell curve by calculus the simple differential equation y' + xy = 0 with y(0) = 1 has a solution y = exp((-x^2)/2) the classic Gaussian function.
Optimum population will be the peak for the combined system divided by x.
That seems too simple. Given enough energy the population could be pretty high, say in a cold-fusion world.
The number could be too high to be realistic. If the energy is high enough the heat output alone becomes deadly.
Any definition of Optimum population should be concerned with pollution or habitat lose.
If I remember correctly, yeast can die by its waste product (alcohol) long before it runs out of sugar.
Boof,
The problem is that everyone always tries to derive the Hubbert curve based on a differential equation, usually via the Logistic equation.
That is misguided, IMO, as it actually is better physically derived via probability arguments of random discoveries. I went through the derivation in a top level TOD post a few years ago.
I recall Staniford pointing out that identity as well (and I have it documented). The problem is that, like the Logistic, it has this strange property of matching the curve well but not making a lot of physical sense.
The bottomline is that curves that describe a probability should start with probabilities, which include things like prior, joint, and conditional distributions.
Very good observation though, and the thought that drove me to look into this topic several years ago. I believe that the actual theory will get proven out one way or another in a few years when more data becomes available. In other words, the forensics will be complete after the patient is dead.
I did some computer simulations of world oil production a few years ago, starting at the bottom up from the well level, using what I know about well decline curves, reservoir characteristics, and the way oil fields are developed by oil companies.
Under any reasonable assumptions, you end up with some kind of bell-shaped curve, although what kind of bell shaped-curve I don't know. It could be a logistic curve, it could be a Gaussian curve, it could be another kind of curve. They all match the simulations fairly well.
This model lacks physical depletion component of renewable resources similar to the one of non-renewables. It describes "ideal" renewables, but we haven't ones at the moment.
"Inputs in the form of human-made-capital (HMC), S2, are the physical plant that must be put in place in order to extract energy from the environment, e.g., oil wells, wind turbines, hydro dams, etc.". And replacing that S2 inputs to extract renewable energy from the enviroment may demand more and more energy while depleting non-renewabls which are used in the process (and that means less and less EROI in the future).
Herman Daly on Nicholas Georgessu-Roegen, an economist who discussed the significance of declining resource quality
http://www.mountainskygroup2008.org/reflections/files/Daly-chapter-11.pdf
Thanks for the link. Hadn't read it in a while.
The scary thing is that the Solow-Stiglitz view of the world is still the prevalent one, and implicitly used in all kinds long term, big picture decision making and advice.
Rgds
WeekendPeak
I think you're conflating the EROEI of a renewable resource with the aggregate EROEI of a society that is transitioning from high EROEI non-renewable resources to lower EROEI renewable resources.
Put another way, there is no particular reason to believe that replacing the S2 inputs to extract a certain amount of renewable energy will demand more and more energy absolutely over time. What seems more likely is that it will demand a higher and higher percentage of a society's gross energy production. The EROEI of the renewable resource, looked at independently, may (or may not) change in either direction during the process.
To make S2 not to rise while replacing aged turbines, panels or dams we have to recycle every natural resource which is used in the process, otherwise the energy cost of production of non-recycled resouces will rise. That means that we have to exclude mining (except some superabundant resourses like sand). Absolutely or very close to. Or make our renewable energy plants eternal. Until we don't EROEI will fall, the only question is how quickly. And I don't think that excluding mining or creating eternal solar panels is a simple task.
And yes - as you said, it will demand a higher and higher percentage of a society's gross energy production (that means society's total EROEI will fall also). There is no contradiction here.
Why?
Depletion of non-recycled resources implies that. Like oil depletion, the same pattern. Exploring rich and convenient deposits first takes relatively small amount of energy, then exploring poorer and less convenient deposits generally takes more and more energy to produce the same amount.
You seem to be asserting that 'real' renewables (as opposed to 'ideal' renewables) won't utilize primarily recycled materials. And you also seem to be asserting that most of the natural materials that go into these 'real' renewables have already entered the decline phases of their production. I'm not sure what the basis would be for these propositions.
Further, I still think there is a conflation between the EROEI of the renewables and the aggregate EROEI of society. The amount of re-cycling is part of the latter.
It seems to me that the EROI of renewables could rise for quite some time on the technological component even as the aggregate EROEI of society declines along with natural resource production. For that matter, it could rise on increased re-cycling.
In particular, we have the standing asset of simply massive amounts of glass, which can be converted in a number of simple processes into 'low-grade' solar heating tools that would be entirely adequate for space-heating, washing and some cooking in residential and in a great many business situations. (As well as water sterilization, desalination and numerous drying processes)
That variety of potential forms and the "Low Grade" banner makes it difficult and unattractive to bother calculating an EROEI number for such humble renewable energy collectors, and yet both the abundant resources that could be accessed through recycling, and the volumes of applications that this could be applied towards makes for a renewable which, owing to the durability of glass itself, and the 'production credit' of that glass's previous service would have an extremely high EROEI.
Even while it's not doing the work of transp. fuels or creating grid power, it would be DIRECTLY doing work that is currently being handled by Oil, Coal, Gas and the Grid, and at an EROEI that greatly outstrips those sources. (Or at least, somebody suggest to me how it wouldn't)
For a simple start on some numbers, I found a wiki reference to Glass having an embodied energy of 16MJ/kg , or 15,165 btu, if the conversion went right, and that Wiki page didn't specify if that was plate glass or not, so this is very loose..
.. while one flat-plate mfr, Sunmaxx claims
while another Wiki page on glass confirms the aging ability and stability of glass,
So it would seem that glass-based Solar Heat collectors could easily have a very high EROEI number, as well as being largely reusable and repairable.. if, in fact, some 10 kg of glass has already recaptured in Sunlight, its embodied energy within a few weeks, but can be able to sit in that sun for many, many years..
Ivanhoe quotes Hubbert on the nature of the curve, 1997.
http://hubbert.mines.edu/news/Ivanhoe_97-1.pdf
Hubbert essentially gives the "specs" for how the curve should be derived. He doesn't actually give the method but includes all the salient characteristics:
The middle part is the aspect that is most troubling, the fact that it doesn't have to have a single maximum nor be symmetric is confounding.
What is interesting is that the combined dispersive discovery and shock model covers every aspect of Hubbert's requirements. It allows:
1. An exponential increase
2. An exponential decrease
3. Can have several principal maximum or plateau
4. Does not have to be symmetrical
5. Is driven by data
6. Is the result of superposition of production from thousands of separate fields
That is the first time I had read that section of Hubbert and in retrospect it gives the reason that the model fits so intuitively well. All Hubbert lacked was the correct math formulation, and he preferred to leave it as a graphical abstraction. The use of the Logistic to map the Hubbert curve covers only the first two requirements. That is why the Logistic alone works so poorly and has not been able to map the plateau we are currently experiencing.
Bit of a no brainer to the average joe thou... I think common sense can be misleading as the truth of some situations is counter intuitive. However depletion of finite resources is not a subject that requires a deep understanding quantum chromo dynamics.
Guessing that there would be a bumpy plateau in production wasn't hard to foresee [thou perhaps harder/more complex to model mathematically from your POV].
This from peakoil dot com pre may 2005
http://peakoil.com/forums/the-opec-thread-pt-1-merged-archived-t160-375....
I suppose this just highlights how thorough this problem is been examined which I think is a sign of denial by large swathes of society. I mean finite resource is not a hard concept to get your head around and peak production only marginally more so.
Sometimes I can't believe I am part of some minority given how bloody obvious it all is.
BTW Good OP for me[others] as the appgopo event in march is on EROEI
The shock model puts that intuition into a mathematical formulation.
Nothing else comes close as far as I have come across. Certainly lots of people have intuited this.
Great tool I have translated it into easy german at: http://www.be24.at/blog/entry/671511
[Edit - English translation of article title is "The lever on the capital employed in the oil sample"]
There is a flaw and a point of confusion in this methodology. Expenses are not taken into consideration. This is a point of confusion among tax specialists, accountants, ordinary investors and even scientists. It is a very different can of worms from 'capital' (S2). It includes expense for labor, taxes, debt service, maintainance and inspection of capital, and increasingly land and water remediation. Perhaps the authors believe expense can be prudently factored out of earnings tied to the production or extraction of energy. Fair enough, as the market value of each dollar of energy should deliver a certain net kJ/$, and ultimately, a good EROI analysis should account for an inflation adjusted avg. dollar value per kJ. But there is a great deal of capital inertia in energy intensive industries. It is well known that the US steel industry would never 'throw away' its plant and equipment no matter how uncompetitive that was --instead labor is kept on at a maximum rate until the company could no longer afford new investment. Same is true for the auto industry which thinks of nothing better than fair exchange rates to sustain it, not labor saving techniques. A recent green argument is that traditional energy sustains itself by recycling old capital and sustaining old payrolls. Alternative energy they say, will enable us to throw away pipelines, refineries and even railroad tracks leading from coal mines to steel mills, to the point where net energy demand will actually decrease, because a greater proportion of demand will go to direct consumption, not rebuilding of capital.
I'm saying that the math analysis presented here will make more sense if it accounts for perpetual and increasing expenses over time, which should implicitly account for capital inertia, and the growing apparent obsolescence over time. A real oil man might argue that there is no real obsolescence of an oil field, and that many expenses such as labor are better controlled here than in the steel and other industries. But we won't know for sure unless the data is laid out in terms of an expense sheet, and not the relatively abstruse concept of 'capital' laid out here.
When I look at Figure 1, I seem to see 'S2' including all those things. 'Capital' is just a shorthand.
"Modern society currently uses around 500 exajoules"
- per second? per year? A writeup of this nature should be more careful of units than the typical journalistic blunder.
"Decline in the physical component of EROI for renewable energy sources represents the likelihood of the most optimal sites being used earliest. For example, deployment of wind turbines presently occurs only in sites where the average wind speed is above some lower threshold and that are close to large demand centers to avoid the construction of large distribution networks. Over time, the availability of such optimal sites will decrease, pushing deployment into sites offering lower energy returns, which should be reflected in declining capacity factors over time."
I appreciate the reasoning here, but real world validity of this may be somewhat questionable, especially at the outset. Why does Germany have so much more PV than Arizona?
Just sayin...
jag - Good point. Part of what I was trying to get across with my long winded comment above. The EROEI of any project (even if you knew exactly what that value might be) doesn't mean it will be done sooner than a comparable project with a less attractive EROEI. Essentially similar to our qualification of PO: geology is important but there are times when the "above ground" factors will dominate the situation. Another example: Mexican Deep Water GOM oil potential. No one knows but let's assume Mexico has billions of bbls of DW oil with attractive EROEI's. Companies have discovered huge reserves right on the US/Mexico boundary. But due to the Mexican constitution foreign companies are prohibited from developing those fields. And PEMEX, for technical/financial reasons, hasn't been able to exploit them. Sort of like the question about hearing a tree fall in the forest if no one is there : if a field has a potential EROEI of 60 and isn't drilled what is the actual EROEI? Easy answer: zero. I have no idea but maybe the EROEI on the Mexican side of the line is better than on the US side. Doesn't matter: US DW oil production is a significant component of US reserves while Mexico isn't producing one bbl of DW oil.
Or to put it succinctly, policy is a wild card that the model will have difficulty accounting for.
And yes, of course that wild card applies to non-renewables and renewables alike.
Perhaps that the difficulty in this debate lies precisely in the fact that the above ground factors are harder to apprehend and to factor than the geological story, which, even talked about with advanced and abstract formulas, is rather intuitive.
I mean, the complexity and dynamics of our whole system are far more subject to fluctuations than what lies in a field and how it can be recovered, geologically and technically speaking.
You well explained in an above post that ER/(money invested) drives production more than EROEI.
Imagine a world where policy is only driven by optimizing energy production and softening energy descent, and is not phagocyted by finance. Strict EROEI would then truly be a reliable variable. But this not the case. And I am not optimistic about whether a simple concept of EROEI can be brought in to anticipate energy production. Until the system as it is conflagrates, the headlong rush to maintain BAU will require that finance takes over more an more, which will soon hit the wall. So until PO begins to unravel its consequences without any doubt for anybody, some of its theorical components (such as EROEI) may not be easy to be recognized and understood by masses.
But then when the system crashes, who cares anymore about EROEI, if there is no more possibility of money investment ? Seems to me that energy is the ultimate wealth mesure unit, but that money has become too critical to our ability to use our energy potential.
Not sure if I well expressed my thought, since I am a biologist by education and that English is not my mother tongue.
By the way, you seem to be one the guys around here with the most impressive knowledge about both geological and financial aspects of oil production, and, referring to the numerous posts in one of the last drumbeats, I want to say that you and other great contributors at TOD have unvaluable contributions for improving my own knowledge about PO. I think TOD is one in the top 3 greatest sites I come across on the web.
youbati - You express yourself very well. "...if there is no more possibility of money investment?...Seems to me that energy is the ultimate wealth mesure unit, but that money has become too critical to our ability to use our energy potential." And IMHO that is THE stumbling block to the general discussion. Fossil fuel resources are critical to the populace and national security. But neither the people or the govt can have much influence. Unlike most other countries those resources belong, for the most part, to indivudual citizens/companies and their development is controlled by private/public owned companies. The objectives of these two groups might not represent the needs of the rest of the citzens or the govt. That's the nature and potential downside of a free market system. A public company is mandated by federal law to maximize benefits for its shareholders. But what if that effort is counter productive to national security or the health of the rest of the economy? ExxonMobil can't sell its products for less than market price without being sued by its shareholders and the federal govt. The govt can put price controls in place but what if that reduces investments and thus decreases future supply availability. The govt can't force companies to make investments. It can produce tax laws and regulations that might encourage such investments. But as we've seen such efforts quickly become political theater.
That's why I think that if "we" want to solve the dreadful equation and revert our route to the cliff, the road map would be left with very few options :
1 behead the market hydra
2 engage in a 180° thinking shift
That won't happen, because there is no chance of reaching a critical level of awareness. Ironically, a fair number of the hydra's heads are no more aware than the average peon.
Anyway, that does change nothing. I'm beginning to think that we are locked in a fatal trajectory.
Either the system crashes from internal contradiction (uncontrolled deleveraging kills the cash cow), or it is put down because of huge worldwide spread social unrest (even if both are linked). The outcome will be the same, the potentially recoverable energy quantity will be halved or so, and we will never recover the financial and technical capacity to reach again current energy production level.
Alternatively, the system painfully achieves to maintain itself for another 20 years (which I don't believe). Rinse and repeat.
Just as if we were playing poker and we got only a few bucks left. We know we'll end the game with nothing, but desperately hope to get the royal flush and then we stay at the table.
That's really staggering.
Talk about rivers of honey and hundreds of maidens.
"Just as if we were playing poker and we got only a few bucks left. We know we'll end the game with nothing, but desperately hope to get the royal flush and then we stay at the table."
That's one of the better descriptions that helps to quickly visualize (and visceralize) this predicament that I've heard lately.
I think a gambler is hidden in every man. If the gambler inside you never shows up, then you are truly a wise man amongst the wisest.
Well, to use the Kenny Rogers song for a guidepost, I would say that we are all gambling in life. We simply have to make our best bets here and there, and use our Spidey-senses the best we can to play each hand, sometimes (frequently) dive right into the unknown as we try things out, make a choice, sign a contract, take out a loan, follow a job or a spouse across the land..
I just think your initial statement reminds me that there are those who may not know when to fold 'em, and when to walk or run away from the table.. indeed, to do any of those things has become unthinkable.
Nice piece of work, I enjoyed it.
However, I wonder just who the target audience is, exactly. Or if that has been discussed.
The use of the acronym EROI to refer to ER/EI is generally a "tell" that it's by academia for academia. In the real world, EROI means "energy returned on money invested". Really, ask anyone. However, a convention was apparently established within academia to use EROI, and in the world of academia that's apparently all-important. Papers must conform to the conventions of previous papers, must they not? A matter of protocol, social capital, tenure track, etc?
So we have what seems to have been a rather exhaustive project to elucidate ER/EI, presented in a form which is nearly guaranteed not to leave academic circles without being confounded with an acronym already in use by economists, investors, and the general public. And worse, it doesn't mean something entirely different which would allow contextual clues of the error, it means something just confusingly similar enough to bollix up most real-world conversations.
This may seem like a minor point. It really isn't.
Pick the low-hanging fruit first. The EROEI is better.
greenish,
Your perspective about the distinction between academia for academia, and the rest of the world is well taken. But I wonder if you are aware of its long and checkered history. One highlite, or nadir, if you prefer, was the episode of Chemistry Nobelist Soddy wandering off into Economics and Theory of Finance. He seems to have convinced himself, and more than a few others that energy is the only 'true' money, and that gold was a false currency foisted upon us by financiers. He was, along with Hubbert, an early promoter of 'technocracy'. It was, I think, Soddy, who invented the word 'technocracy'. The word denoted an invented form of government that embodied his ideas. Confusion of money and energy has a long and muddled history. Trying to unmuddle it by suggesting neat distinctions --- is unlikely to succeed. There are, in both finance and academia, forces (read people and groups) that thrive on intellectual muddles.
I think the confusion is deliberate on the part of the original authors and cannot be attributed to TOD staff: the original paper title is "A Dynamic Function for Energy Return on Investment."
Thanks, I recognize that the TOD staff are just going along with the original authors, who are going along with authors before them, etc. My point is that if one is hoping to clear the waters and see the concept in wider use, it would be good to refer to it in a non-confusing way.
The fact that money and energy are often conflated and confused is the whole point. I have many times seen discussions by smart folks veer from one definition into another with people talking past each other. Which is a shame, because the concept of ER/EI is an important one and is nowhere near mainstream. Thus at the level of political decisions we get silly subsidies like corn ethanol, and presidential candidates claiming we have multiple Saudi Arabias of new oil in the USA if only the laws would let us drill.
I like the keypost, it just seems a shame to see the concept hobbled from the getgo by an inherently-confusing name, and would like to see authors publishing on the subject take a step outside academic timidity for the sake of clarity.
Really they need not. All you need is to put clear definitions in the beginning of the paper. You can still put EROI in tags so people who are looking for that will find it.
Thanks, that was my point. I was attempting to affect an ironic tone in describing an "imperative" which is anything but. What you describe is exactly what I'd like to see, and it shouldn't create any immense kerfluffle. It's good for scientists and academics to take reasonable steps to make their work user-friendly to those outside their discipline.
BTW Jben, you've become one of my favorite commenters, kudos on what you add to TOD.
Thanks, no problem. :-)
I haven't read Cleveland paper on the Louisiana fields so I'm not sure of how he was using his findings, but thermodynamically the ERoEI of a field can not go up. That would imply that more energy was being input into the field than was being extracted. For the ERoEI to increase without an input of work would be a violation of the Second Law. The ERoEI change of oil fields results from a change in the entropy of the system; it requires an entropy gradient. For the field the entropy goes down as crude is extracted, and for the entire system (field and environment) the entropy goes up. Cleveland's findings probably resulted from a bookkeeping anomaly using an Energy/Cost evaluation, that is, it resulted from how the initial investment was depreciated.
That being said, the authors use Figure #4 which shows an initial ERoEI increase as a bases for determining the PDF (probability density function), which morphs into what that looks like a Power-Pareto or skewed Logistic distribution. Either way, the QQ Plots of these distributions against the world production data-set give very unsatisfactory fits.
Without more validation of the hypotheses from which they are working, not much validity can be given to it concerning oil price or production!
Maybe I am confused here, but isn't the ERoEI of a given field a function of the technology employed as well as the geology of the field?
It is possible to apply more efficient technology to an existing oil field, so that more energy is extracted than with the old technology, for each unit of energy invested. More efficient pumps, better drilling technology, etc.
Of course, very often new technology is employed that extracts more of the reserve but at a lower ERoEI, but there is no thermodynamic constraint.
Not sure whether a all things being equal assumption is made here.
IE the technology always degrades the theoretical maximum given perfect recovery thus isolating a value for the geology? better tech is a post geology modifier moving you towards =1?
EDIT
the tech can never break the theoretical minimum extraction energy cost it can only move us closer to it.
the tech can never break the theoretical minimum extraction energy cost it can only move us closer to it.
Well, no, that's not true. Technology can break the theoretical minimum energy cost by using a different and more efficient theory. That's the whole point of technological innovation.
that would imply some sort of modelling error in the boundary conditions?
EG: if you have a space craft the maximum efficiency of any onboard fuel is theoretically bounded to some sort of anti matter drive with 100% efficiency. any improved tech will move towards this optimum
however you could push the craft through space with some sort of off board fuel [solar sail or lazers etc].... moving the goal posts [but lowerimg the EROEI in this instance]
for the sake of this post the assumption is there is some sort of lower boundary AIUI on the minimum lifting energy that tech can not break.
I am not too sure what you mean by more efficient theory? More efficient application or technology I get. Theory implies some deeper understanding of physics or some such ie scientific as opposed to technological breakthrough. not sure if that is what you mean.
Oil fields are not like spaceships. When you are talking about the ERoEI of recovering oil from an oil field, you don't actually know the boundary conditions, and there are breakthroughs in improving the efficiency fairly often.
Rocket engines are pretty much the same as the ones they used to get to the moon, and the US no longer has rockets that can get to the moon anyway, whereas the oil industry has come up with hydraulic fracturing, horizontal drilling, steam stimulation, 3-D seismic, and a whole host of innovations that make the process of finding and recovering oil more efficient. The pumps have become better, too. These have considerably improved the ERoEI of the process.
The only thing is that almost all the easy oil has been found, and oil companies are going after oil than would have had too low an ERoEI to be recoverable using the old technology they had back during the Space Age. But there are no theoretical lower limits on the energy needed to extract oil from oil fields, only practical ones, and practical ones can be broken with new technology.
I would suggest somewhat childishly that raising any mass by x meters is a lower boundary
if 1 kg of oil is 100m underground and needs to come to the surface mgh=1kgX10[9.8 whatever to be picky]X100m= 10,000J
some or all of this energy may be stored in the oil deposit by geological forces in the form of pressure [or not] but that is a min energy requirement to lift that oil and represents a lower boundary. no?
The oil is under pressure (oil fields are water drive, gas cap drive, and/or solution gas drive), so the energy to raise it to the surface is comes from the oil field itself and is not part of the ERoEI calculation.
Once the reservoir pressure is depleted and the field has to be put on artificial lift, yes then there is energy required. However it is typically not large compared to the other inputs to the ERoEI calcuation.
well I would have thought the declining EROEI of field is highly attributable to the reservoir pressure and be very much part of the calculation.
but I will defer to your superior understanding
By theoretical minimum costs, we mean minimums calculated according to fundamental mathematics of physical laws, not descriptions of current technologies. Carnot efficiency is a good example of theoretical maximum efficiency for a given type of problem.
In the case of oil (that is not under pressure), no technology will ever get minimum energy cost below the gravitational potential energy added to oil when it is raised to the surface of the Earth from below. There is no 'more efficient theory' to be found here.
So it really is true.
Ralph - If we talking about total field EROEI I can give a real example that will hopefully prove the point. A field in Texas has produced 32 million bo (45% recovery factor). But it's down to 14 bopd from 6 wells today. So it's EROEI is set...what every number that actually is. I'll be drilling two horizontal wells to recover some of the residual oil. My individual hz wells may do 200-300 bopd. If I'm correct about the potential recovery the EROEI of my wells will be much better than the original wells.
So it might be more of a philosophical question: if I'm correct did I just improve the EROEI of the field overall or did I just conduct a new effort with a much better EROEI than the original development? There are other methods that can improve recovery economically. But with the possible exception of my project or water flooding I suspect the incremental improvement in EROEI would be rather small.
Ralph
I think your post is totally correct. Thermodynamics does not determine the efficiency of the technology that humans employ for production. Humans do. It is absolutely possible for EROEI to rise at some point or another.
It looks ok. The EROEI can increase because of latencies in the impact of the original setup. There is a phase in the production called maturation, where the production catches up to the investment.
I am not sure how you are using entropy. Is it in the information entropy sense?
So if we have a model of how EROEI changes over time, can we make a guess at what the curve is for oil?
1 - 1/EROEI is net energy right? So we could scale historic oil production by net energy to see whether/how far we are past peak net energy from oil? And how steeply net energy goes down after the peak?
If anyone does create that graph, please label it "Scary graph, don't look at this Jon".
Thanks in advance...
Jon.
j - Not a simple as I first thought. Assume Field A has 10 wells and the EROEI the first day of production is 30. But to calculate that number you have to use expected URR of that oil. In one sense EROEI is easier to model confidently than the economics if for no other reason is the difficulty in predicting future oil prices. of course, URR is often not as accurate as we would like. So one Day 1 the EROEI is 30. Why if we've estimated URR and energy used during the production phase why would EROEI change over time? Wouldn't it be the same as the day the day the field was depleted? Seems so to me.
OTOH if I came into the field when it was half depleted and applied some new technology that increase URR by 20% do you recalculate the EROEI with those new reserves less the energy budget to add them? Seems reasonable. So now you have a chart of EROEI vs. time that's a flat line up to the point where I apply my new tech and the curve takes a stair step up and continues it flat line.
Does that make sense?
I think I misread your post. Are you asking how EROEI changes industrywise?
Rock, yes, I'm talking worldwide. Reduced global EROEI means that the downward slope of a global Hubbert curve is understating how serious things are - net energy is falling faster than gross oil production would suggest (even before you've factored in the decreasing energy value of an average barrel and increasing global population).
I guess I'm taking some pretty detailed mathematical paint and applying it with the broadest possible brushstrokes... apologies to the model authors for that!
Jon.
Jon - Yep. After blabbing away I thought I might have missed your point. But consider this line of reasoning. Folks say EROEI is heading to the toilet because all the "easy oil" has been found. I don't know that oil has ever been easy to find. You can look at a map of the Texas Gulf Coast and wonder how easy it must have been to find those fields. But you don't make a discovery unless you talk someone into drilling a well. And that has never been easy IMHO. At least in my experience over the last 36 years. And when you did discover that big field it still cost energy to develop it. Say 50 years ago I found a huge field that required 200 wells to develop. And this year I find a small field that takes only 5 wells to develop. So which field has a better EROEI? Who knows. Maybe the big one...maybe the little one...maybe the same EROEI. The old field will produce a lot more oil but will also take 40X as many wells (and energy) to develop. And that's what EROEI means, isn't it: how much energy is utilized to produce the energy gain. Maybe the old field took as much energy to develop PER BARREL as the new one?
And consider this factor: I may have drilled 10 dry holes while hunting for that big field. Fair to use that energy expenditure to calc the EROEI, right? But I only drilled one dry hole to find my new field thanks to modern seismic technology. I might not be able to find as much oil today as I could 50 years ago. But I can find what's left much more efficiently than I could long ago. And that efficiency means a lower energy budget.
How about Deep Water fields? Takes a lot of energy to build those huge offshore facilities. OTOH my old big field flowed an average of 200 bopd from each of those 200 wells but my DW wells flow 5,000 bopd each so a lot fewer wells.
Instinctively I would think EROEI has decreased over time. But I suspect that if you got all the details together it wouldn't be as dramatic as some assume.
Rock - Maybe it might be time to consider blacker pastures in the pursuit of oil? Surely if you consider any other oil producing region in the world it has been explored far less than Texas has.
Rock & Jon
I hesitate to join in this late and with only a one cent contribution in my pocket.
Maybe too simplistic?
Will it help define EROEI if we assume that, for the sake of argument, 'the world' must (or even just the USA ‘must’) continue obtaining oil at the same rate as now, and that this rate should deliver at least the same utility as now? (Very useful stuff oil. One could perhaps add a rider that preferably, the world should continue to produce a little more each year to satisfy unmet demand.) [EDITED above para]
Assume also that as of now most oil grades still produce some varying but satisfactory fraction of gasoline, diesel kerosene etc etc.
However, we know that to keep up the total numbers for the products (and for their utility), new sources are always needed.
These newer sources could include, for example, 'difficult to refine' oil with lower utility per barrel?
Also we have other new categories. Am I for example right about the following? We know that most deep ocean oil for example depletes faster than say dear old Ghawar; even depletes faster than Texas did on aggregate during the oil-rush?
Tar sands, useful stuff, could be another example. We know these take a lot of energy to produce, say a return of 7:1. Biofuel from oil-seed takes even more, even though the sun is counted as free, giving say a return of 3:1.
So, over time these new sources, especially if they on aggregate deplete faster, must be produced at an ever expanding rate to keep up with depletion of original sources, and at any one time require an ever increasing fraction of the total possible 'world industrial activity'? And thus to meet the world target will require an ever increasing fraction of the world's use of the produced fossil energy? You can ramp up new faster-depleting sources as much as you like, you can supply half the USA from as much tar sands as you like, and even grow whatever it takes of oil seed, but you are going down a steep cliff of diminishing returns?
best
phil
Hey all,
Thanks for taking the time to read my paper. Thanks also for the comments.
This paper is basically taken straight from my PhD thesis - hence is pretty technical. Not written for a general audience... Sorry for that.
For those interested, you can read the rest of my thesis and other publications along similar lines here:
http://stanford.edu/~mikdale/Michael_Dale/Michael_Dale.html
Cheers
Mik
RalphW said:
ERoEI = EG/(EG-EN) where:
EG = internal energy (Uin) of a unit of oil in the well (assumed constant for any field)
EN = internal energy (Uout) of a unit of oil after the energy required to extract it has been subtracted
Internal energy is a property of matter. Where a property is defined as: "A quantity is a property if, and only if, its change in value between two states is independent of the process". Since ERoEI is the product of properties it is also a property; by definition.
According to the equation above the ERoEI (since EG is assumed constant) can only be increased by increasing EN, which by the Second Law must be EN < EG. To increase EN the efficiency of the extraction process must be increased where: Eta = 1 - Uout/Uin. To increase the ERoEI of a field from 10:1 to 15:1 would require an increase in Eta of 33.3%. A decrease in extraction energy cost from 14,000 BTU/gal to 9333.3 BTU/gal - a 33.3% decline!
Oil extraction technology is a very mature technology; over a hundred years old. The chances of increasing the efficiency of the extraction process by even a few percent are very small (otherwise the the producer probably wouldn't be in business to start with - it took the refining industry over 40 years to improve its efficiency by 30%). The cost of retro-fitting even very old fields would rarely be compensated for by the small increase in ERoEI that might be attained. As an example, to increase the ERoEI of a 100 barrel a day well (more than 50% of the wells in the US produce less than 10) from 10:1 to 11:1 at 7000 BTU/$ on a five year payback would have to be done for less than $1.3 million. $1.3 million will get you two 30 hp deep water (high head) submergeable Flite pumps and a pickup truck. For most situatations the energy cost of upgrading will be higher than the energy savings. The technological limit is the maximum theoretical efficiency of the extraction process (which has long since been approached).
Since ERoEI is a property of matter it is regulated by the same thermodynamic laws as all properties of matter (mass, energy, entropy, etc). For any real world application the ERoEI of a developed oil field can not go up!
Nobody disagrees with you regarding the EROEI 'developed' fields that are already using the most efficient technology available. However this does not correspond to all 'real world' situations, and it is not the totality of what the authors are trying to model.
The model being proposed is attempting to model various resources from the beginning of development, not just developed oil fields. It assumes that at the beginning of the development of any resource, the extraction technology being used will not the most efficient.
EROEI is not a property of matter, because the energy used to extract energy is not a property of matter. There is a human/technological factor. So EROEI is not %100 determined by thermodynamics. The model may be inaccurate or simplistic it its representation of the technological element, but it does not violate physics merely because it posits that the efficiency of extraction technology may rise at some point in time.
jag et al - First, to avoid debate where there's really no need maybe we should define a "developed field". The simplest would be a field where no existing or future technology will increase URR. With that I gather all would agree that EROEI can’t increase. OTOH you can’t predict the future. So now I suppose we could call increasing URR in a field after the initial development phase a “new field” but that seems rather misleading IMHO.
With re: to such redevelopment not adding but a few percent URR and not improving EROEI there are thousands of fields that have proven that supposition wrong. I’ve seen numerous “fully developed” fields more than double the original URR by secondary EOR methods. Done often with water floods and less common with firefloods. And at times, but not always, the EROEI of the secondary effort is greater than the initial EROEI. Again, if one wants to classify the secondary effort as a different “field” than you wouldn’t combine the original and secondary EROEI into a composite greater than the original. OTOH Cantarell Field in Mexico may be the most dramatic example. After the field had been “fully developed” PEMEX quickly realized that the URR from this pressure depletion drive reservoir would be very low…maybe just 10-15%. So the initiate the N2 injection program. Just my WAG but this probably increased the EROEI several hundred %.
Of course, in the US, the majority of fields that would have benefitted from some form of EOR have had it applied. But there are still tertiary methods that can be applied to some. By year end I will start a pilot program to prove I can recover a significant amount (5 – 10%) above the original recovery by utilizing horizontal wells. Though these wells will cost much more than the original wells drilled over 50 years ago, the energy used to drill the new wells won’t be significantly greater. In fact, given increases in efficiency over the last half century they might even take a little less….again, energy not capex. The percentage increase may not be huge but I’m also looking at 2 billion bbls of residual oil in just one trend in Texas. Won’t change the future of PO IMHO but that does represent a lot of new grease.
jaggedben said:
Absolutely wrong, all energy, no matter what its source, is a property of matter - by definition. The problem with the study is that it is not reconciled with presently available information, the world production data-set, and it is based on a false premise, that ERoEI can be increased for a developed field.
The ratio of two portions of energy that are used in a human endeavor is not a property of matter. It is partly determined by the human endeavor. Just as the efficiency of a technology is mainly a property of the technology, not merely the fuel that is used.
Your complaint is based on a false premise, which is that the authors are attempting to model only 'developed' fields.
I don't know how to put these things more plainly.
Because this thread will be closed pretty soon, I'll offer one more argument.
Let's suppose that there are two companies extracting oil from two different fields. For the sake of argument, suppose that the fields are physically identical. For that matter, let's suppose both fields are both 'developed', and that the 'latest most efficient technology' is being used.
Now suppose Company A has a diligent and organized foreman who carefully ensures that when extraction equipment is brought to the field, it is done with the fewest trucks required, and in the fewest trips necessary. But Company B, unfortunately for them, hired an inexperienced foreman who always makes logistical mistakes that require many extra truck trips, thus increasing the amount of diesel fuel energy that Company B uses compared to Company A.
Since we are supposing all else is equal, the EROEI of Company A's field is higher than Company B's, because Company B's extra truck fuel adds to 'EI', while 'ER' is the same for both companies.
Now according to you, it is impossible to raise the EROEI of Company B's field to the level of Company A's by hiring a better foreman. That, you say, is because the fields are 'developed' and the ERoEI is a 'property of matter', and the foremen have nothing to do with it. But this simple thought experiment compellingly proves your argument false, while relying on nothing more than the obvious observation that not all human beings are equally careful and organized.
jag - Actually it happens all the time. I'll be producing a field with a high water cut. Cost a good bit of energy/money to lift the production and dispose of the water. Eventually I plug the high water cut wells and reduce my energy consumption but give up very little energy production. But this brings back to question what changing the EROEI of any field over time means. I can do as I just said but in reality I may be changing the ULTIMATE EROEI of the field by just a very tiny amount. Such changes are made in all fields as they head towards depletion via improved recovery efficiency of new tech or the elimination of inefficient wells.
I suppose one way to frame the discussion is that the ultimate EROEI of any field can't be estimate until a field is abandoned. OTOH I may be drilling into abandoned oil fields next year and recovering residual oil at a decent EROEI. Thus I could be changing the EROEI from any original estimate.
Just had another thought. The Eagle Ford Shale play in Texas. EFS isn't a new play. I completed my first EFS well over 25 years ago...not a very profitable vertical well...poor EROEI. I have no doubt someone has re-entered an area of similar vert EFS wells and drilled horizontal wells with much better EROEI...but not necessarily very good EROEI.
Yeah the EROEI figures would need to be compared to fields/wells of equal production rate to have any meaning in the present rather than history.
I suppose the one bona-fide real way to increase EROEI is to reduce extraction rates?
When dealing with variable quantities such as rainfall, it's often better to work with cumulative curves rather than spot values.
Similarly, I think the EROEI of an oil field should be the cumulative one: total energy returned over the life of the field to date / total energy invested.
If the field has been producing a long time, any additional effects caused by new technology will be minor compared to the bulk of energy already produced or invested, so the ratio will become pretty stable over time.
aardi - "...the EROEI of an oil field should be the cumulative one..." Excellent. That's the point I wasn't making clear. The initial wildcat drilling should have a lower EROEI since much of the energy expended is front loaded on the first wells. Likewise with the capex. But as the development wells are drilled the cumulative EROEI will generally improve. Also, as a field is produced you learn more about its specific reservoir dynamics and improve efficiency, hopefully, improve EROEI. And should enhanced recovery methods eventually kick in EROEI can improve even more. But there can be cases when future activities might reduce cumulative EROEI. If oil prices jump up significantly some more energy/capex intensive production methods might be employed since the profit is there. As discussed before the oil patch makes decisions based on ROR and not EROEI. IOW: follow the money, baby. LOL
If you had read my second post in its entirety you would know why the ERoEI of an existing field can not be improved by hiring a new foreman. With technology as old and as mature as oil technology the efficiency increase can only be very, very small, and generally would not be payed for by the increased energy produced. There is a difference between modeling a real world scenario, and some make belief reality; that reality is called the Laws of Physics.