A Nice Counterexample
Posted by Stuart Staniford on October 1, 2005 - 1:21am
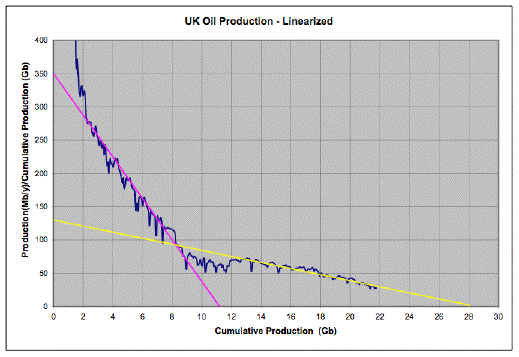
Nick Rouse kindly provided me with an Excel spreadsheet with a Hubbert linearization of UK oil production (the only thing I added was the yellow line). As you can see, there was a long period when the curve looked linear and yet it would have totally misled you had you simply extrapolated it to the axis. You would have thought there was going to be about 11gb, but now it's headed for 28gb. So, things are more complex, and we must see if we can come up with some principle for dividing the Romanias (where this method seems to have worked with amazing success), from the UKs (where it would have been very misleading) before we can feel any confidence in our extrapolation of the Saudi graph or the world graph. More below the fold.

This is referenced from here. Clearly, production initially looks like a nice Hubbertian single peak, but then, whoops, a bunch more oil from somewhere is produced. And the initial (pink) straight line above only knows about the first peak, so when we get this second, superimposed peak it is not accounted for. However, we do go linear again, just with a different (yellow) line going to a much higher URR (28gb versus 11gb).
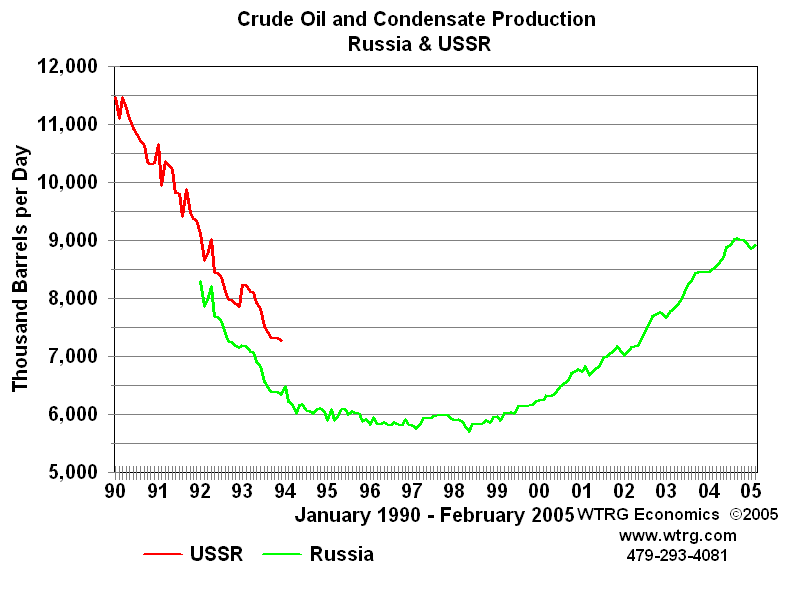
Clearly, we are likely to run into the same general kind of problem with Russian production, where James Williams shows:
In the UK case, economists will quickly be tempted by the idea that oil prices had something to do with it, since the second peak starts to go up again in 1993, a couple of years after the price spikes of the first gulf war. However, it's pretty clear that price does not cause too much deviation from the basic Hubbert model in the US or Romanian case, so we would be left trying to explain why price matters greatly in some places but not in others (especially challenging in the US, center of the free market religion). So this explanation doesn't seem too tempting to me (price seems to explain some of the noise about the basic Hubbert curve, but not the gross features of the shape of the curve).
Nick notes that Jean Laharrere has considered the possibility of discovery as an explanation. Here's Laharrere's figure plotting UK backdated discovery and production:

Clearly, we can see that this bimodal discovery curve looks like a good explanation of the bimodal peak in production. A lot of discovery initially occurs in the late sixties and seventies, and this powers production in the late seventies and eighties. But there's a second wave of discovery beginning after 1980, and this powers the second peak. There's not much of a third wave of discovery, so there seems limited prospect for much relief in UK depletion rates soon.
It's interesting to contrast the situation with that in the US. Laharrere again:

This time we have cumulative production plotted versus time. Pretty clearly, the nice sigmoidal logistic discovery gives a sigmoidal production curve 30 year later. What's different in the North Sea is that production comes on stream much faster - production is following discovery by only a decade or so, rather than three decades. Clearly the world was in rather a hurry to get that oil by this point in history (after the oil shocks of the seventies).
So, here's a new tentative working hypothesis:
Hubbert linearization is a decent approximate model for oil production unless production is interrupted by a societal collapse, or production is very closely following on the tails of a very noisy discovery curve.Clearly, further investigation is needed to support or refute this working hypothesis. In particular, if anyone knows or discovers other countries where linearization works well, or where it fails for different reasons, I'd love to hear about it. Hopefully our resident sceptics will go do some work and come up with some more evidence. But my final thought for tonight is just to look again at the Saudi situation.
Now the discovery picture there is somewhat unclear since we have wildly conflicting information about what their reserves really are. But Laharrere plots a variety of opinions:

Everyone agrees that all the discovery happened a long time ago - 90% of it was before 1970, and two thirds of it was before 1960. So it seems to me that our tentative hypothesis would suggest that linearization should work decently for Saudi Arabia (unless they were to collapse - never to be ruled out in the Middle East). The implications of linearization being pretty much true for Saudi Arabia again:

180gb of URR with 110gb produced already!



(at least for me ) the proper role of Hubbert analysis.
Those additional taxes made the UK, already a high priced exploration and production market (due to the environmental and regulatory climate) a difficult place to justify investment dollars. Big oil investment dollars go to the lowest risk/reward regions of the world. That is why offshore West Africa has exploded in production the last 5 years. Biggest bang for the buck.
Norway's depletion can be viewed in the same way. It is by far the most restrictive place to drill on the planet. We know where the oil and gas is. It is currently not economically viable, given the restrictions in Norway, to drill there.
If I understand correctly, it's because governments don't invest in enough capacity to get the oil out of the ground fast.
Why not?
What you get is an asymptote that always starts at 1 (first year production/cumulative) and approaches the x axis but never gets there.
The chart for the UK and many others looks more like the chart for a `perpetual' oil field than a straight line. There aren't enough data points to distinguish between them so either could be true.
So what you've discovered is that not all curves produce a straight line at all. In fact this seems to strengthen, not weaken the theory slightly, since the curve you identified that doesn't produce a straight line is also impossible in real life.
Chris
It obviously doesn't do a good job for the world as a whole -- as demonstrated by Colin Campbell's failed predictions.
The only value which the linearization method might have is its ability to predict peak oil. Now, IIRC, Deffeyes predicts peak oil for Thanksgiving Day 2005 based on the linearization method, so that's the reality check.
Also, the method isn't objective until you specify an objective algorithm for selecting the line, and apply it uniformly in all cases. Otherwise, it's just subjective voodoo.
I agree with you that the predictions of the world peak are a good check. However, Deffeyes used a particular oil data series (and I don't actually know which one!), and it's only fair to do comparison to whatever series he was fitting too. Also, obviously there's significant noise, so it could well be off by a few years either way (as it was for the US). But I don't believe it's going to be decades off. We need to get to some error analysis here soon to tighten that up (but one thing at a time).
The more I look at it, the more I dislike plotting aP/CP against CP. I once was told a story long ago by my father who described going to a talk by another engineer who was very excited about this great correlation he found in his data set. The data points were very well aligned, all falling along a straight line. Well, as it turned out, the engineer had plotted X against X!
And that is part of the problem. We ought to not contaminate one already dependent variable onto the axis of the other variable -- unless you are relatively sure that this fits some realistic behavior (c.f. the "drunk looking for his keys under the streetlight" scenario). And I think the non-linear behavior we consistently see rules out the logistic model.
I have a post up describing the quasi-hyperbolic behavior that likely fits better here:
http://mobjectivist.blogspot.com/2005/09/oil-shock-model.html
and a more recent post showing how the math also describes the behavior of a simple electical RC circuit here:
http://mobjectivist.blogspot.com/2005/09/rc-circuit-analogy.html
But I also have to agree that the extra bump provided by new discoveries in North Sea oil tends to once again flatten out the slope. After all, every earlier discovery accomplished the same thing!
And don't take this criticism wrong. If you tried publishing this in any scientific journal as I and many others are accustomed to, you will have to be prepared to go through the ringer in your analysis. It's just that referees are much less common on the internet than in academic circles, as it doesn't come with the job description and it won't help anybody get tenure.
I have significant experience getting modeling work published in scientific fora, some of which has been very influential - scholar.google me for details. But these posts are work in progress (as I think should be obvious). No doubt publication will eventually follow when I think I have the story figured out to my own satisfaction.
So is that really how Hubbert, Deffeyes, and others set up the original peak oil math? By using a "predator-prey" model? Oh my, no wonder that people like Michael Lynch and company are having a field day in dissembling these kinds of models. It's common practice in those circles to simply trash another's model (i.e. policy); Lynch then doesn't even have to come up with his own. Look at how well this strategy works in today's political circles.
Fundamentally, it is an empirical question whether or not the model applies to oil production. No-one would claim it's going to be a perfect fit (or no-one with any sense, anyway!) but it has done a reasonably decent job in the very mature production areas (but not in the early stages). Stare at Romania again:
But there are certainly regions where it could mislead you without care (eg the UK). I'm engaged in trying to develop insight into where we might expect it to work, and where we might not.
As to Lynch et al. Critics serve a very valuable purpose in noting the holes and driving the improvements that need to be made. However, it's always much easier to criticise than make some constructive proposal oneself. No-one remembers the critics - they remember the people who make developments that actually improve the state of the art. Hubbert will be remembered far longer than Lynch, even though I respect Lynch as Hubbert's best critic: he has done some actual hard work and made critiques that serve a useful purpose.
And again - if you can develop a better model, more power to you. But the proof of that is showing that you can predict forward with smaller residuals for a broader class of situations.
I don't respect Lynch at all. I agree with many people that think he is intellectually dishonest.
The exponential model works over every regime. It just needs a forcing function to create a spread in starting points.
VERY interesting.... Write a post about this.
Now knowing what the basis of the logistic model was before today, I keep wanting to imagine little Pac-man oil molecules gobbling each other up. I will probably have nightmares over this tonight.
In the normal predator-prey relationships, you can get away with this stuff because you are ony dealing with discrete entities that have at least an empirical relationship. For example, it takes N rabbits to sustain a single fox. Or one virus to infect one unprotected computer. Or an anion and a cation to generate a molecule. But where does this relationship come up here?
Note that the initial UK peak was only about 10 years after the onset of serious oil production. This would be analogous to just looking at Texas data from 1935 to 1945. If you just focused on 1935 to 1945, the plot of Texas data would have given you a similarly erroneous result. Hubbert made his Lower 48 prediction about 27 years after the East Texas Field was discovered.
The answer to the apparent conflict is that the initial data points don't provide sufficient data to make an extrapolation.
Again, in my opinioin this technique works in the real world because--after decades of drilling--the industry has a pretty good idea of where the big fields are.
Jeffrey J. Brown
monthly production had already fallen by 25%
over its peak in January 1985. It undoubtedly
caused a direct loss in production but any losses due
to a reduction in exploration would have shown up
10 years or so later about 1998 when production
was near its second peak
Dave suggested that he would not expect another non-linear deviation but this is not sure.
Contrary to what Mad Oilman suggested, In 2003 the Chancellor of the Exchequer, Gordon Brown announced tax changes in favour of North Sea exploration. See:-
http://www.ukbudget.com/prebudget2003/Prebudget2003_companies.cfm
and this has resulted in a fair boost in exploration. See:-
http://thescotsman.scotsman.com/business.cfm?id=102472005
There are still forecasts that production will rise for a couple of years before starting to decline again although some only hope that it will slow the decline down. Whether this will happen to any large extent is open to doubt. There are some very interesting graphs here:-
http://www.worldoil.com/Magazine/MAGAZINE_DETAIL.asp?ART_ID=2655
Fig 1 shows the modest increase in the number of exploration and appraisal wells that have been dug (not including the expected increase in 2005 given in the Scotsman reference). However fig 3 shows the strong decline in the success rate of exploratory wells dropping from 43% or so for much of the 1980's to 20% in 2004. It would be interesting to see comparable figures for other parts of the world.
The forecast part of the production figures in Fig 3 seems optimistic in the near term as the show a slight increase in 2005 and output has fallen 17.5% in the first 5 months of this year
I read that actual oil production costs are around $0.50 to $1.50 per barrel. Is this true? If so, then tapping smaller 'more expensive' fields after the giant SA fields begin dwindling would raise the price to what? Even $3 to $8/barrel wouldn't really impact current prices. Am I missing something?
H
#1 They have peaked in light sweet production (according to their own journal) which means additional production increases will only come in the form of heavier, sourer grades that are harder to refine, etc.
#2 The infrastructure to drill the wells, build the pipelines, etc. is just not nearly as far along as in the US. If we want to lay down a ton of wells, etc. in a field, there are all sorts of people to do it. For most of SA production history the oil has been flowing from a relatively small number of wells considering the size of the fields.
And I'm also loathe to believe that the recent upward reserve revisions are based in anything remotely approaching reality.
I don't understand why this indicates a lack of new fields. Many of the fields being reworked were partly developed and then mothballed due to low prices. Why wouldn't the Saudis go back to them? What's the alternative? Just ignore them, and leave them there half developed forever? If they already have some infrastructure, it's economically rational to return to partly worked fields first even if they have plenty of other fields.
Regarding production costs, I don't know if anyone outside Aramco really knows what they are, but given the extensive waterflooding and maximum reservoir contact (MRC) horizontal wells, I'm sure they're higher than $1.50. The bottom line here, though, is that production costs don't really impact what traders pay for a barrel of oil.
In 1972, almost everyone (except Hubbert) assumed that Texas could increase production at will--just as most people assume today assume that SA can increase production at will.
The Texas RRC went to 100% allowable right around 1972, the year Texas peaked. Prior to that, the Texas RRC had controlled production in order to keep prices stable. By the way, there were attempted Arab oil embargoes prior to 1973. They failed because the Texas RRC flooded the market with oil.
Texas had a frantic drilling program after 1972 that did nothing to reverse the decline, even though the number of producing wells went up by 14% in the 10 years after 1972.
But the bottom line is this. The Hubbert method (assuming a peak at 50% of Qt) picked the Texas peak within two years. This may be a little misleading. If we assume that a more accurate prediction is at about 55% of Qt, the Hubbert method picked the peak year exactly. SA is at 55% of Qt.
Jeffrey J. Brown
Of course, the decline referred to in Abdullah Saif's statement could be the equivalent of Skrebowski's "Type 1" decline: certain wells are declining, but production is maintained by drilling new wells or increasing flow rates from other wells at the same fields. In other words, production would fall 5% to 12% in a year at existing fields if they weren't worked on. However, if total production from those fields is actually falling at that rate and can only be replaced by new production at other fields ("Type 2"), that is alarming. Unfortunately, "Type 2" decline may be the correct interpreation of Abdullah Saif's statement.
Hate to be blunt, but this is the very definition of conspiracy theory.
It's also self-serving that you claim the Saudis are liars, and then immediately proceed to quote a Saudi official to support your point. Isn't Abdullah Saif a liar too? Surely he was at the meeting where the Aramco executives pored ashen-faced over the data and decided they had to lie to the world. How do you explain the fact that the truth leaked out?
Or is this just a case of cherry-picking? I.e.: When the Saudis say negative things about their production, that's true; and when they say positive things about their production that's a lie.
I do not know which if any Saudi statements are true. I was pointing out that one set of Aramco personnel in one context claimed they were managing their fields for 1% to 4% decline and that we should be reassured by this as to the future performance of their production, while a different official in a different context stated that they were already experiencing 5% to 12% decline in their fields. This seems like an inconsistency, and a severe one, on something that really matters. At least one of these statements must be misleading. Similarly, one set claim they had 700gb of OOIP, gradually increasing from 570 twenty five years ago, while almost simultaneously, al-Naimi is saying there's 1200gb of OOIP. I don't see how they can both be truthful statements of their best understanding.
I tend to think there is somewhat more likelihood of things they say that are contrary to their interests being true. But really, having concluded that they are not committed to providing accurate information to the world, I prefer to reason as much as possible with information that doesn't come from them. You yourself have stated that you believe Sadad al-Husseini, which presumably implies that you do not believe the official Saudi position that they can produce 15mbpd for 50 years.
The deeper issue is this: We always talk about transparency in the context of Saudi Arabia. Simmons pays lip service to transparency for everybody, but he invariably hammers the Saudis. In fact, I don't think I've heard him, or anyone, explicitly go after a country other than Saudi Arabia.
How about transparency for Venezuela, for instance? The U.S. currently imports almost as much crude from Venezuela (41 mb in July) as from the Saudis (46 mb in July). Why doesn't Simmons hammer Chavez? Are we getting the truth from Petróleos de Venezuela?
Take it a step further. Suppose we inspect Venezuela. We send in the third party inspectors, and they determine that Venezuela indeed has plenty of reserves. The problem isn't the lack of oil; it's the lack of a favorable investment/production environment. Chavez is scaring away all the big oil companies, giving investment the short shrift, and funneling all the oil revenues to the poor, Cuba etc.
What's the verdict then? I'm afraid the answer will inevitably be: get rid of Chavez, we need that oil now. Oil is essential for our economy and our military, and doing nothing is not an option.
I don't want to see things go that way. My agenda is to leave as much oil in the ground as possible, for as long as possible. Anything which hinders oil production is good IMO because it's good for the atmosphere, and it accelerates the process of adapting to less oil. So I think it's counterproductive to support a campaign like transparency because it's an attack on the prerogatives and sovereignty of nationalized oil.
That is why I don't care whether the Saudis are lying. The Saudis aren't the problem. Peak oil is a problem which must be solved on the demand side, not the supply side.
Maybe. There's also a good chance that transparency will reveal the situation to be just what Al Husseini says it is, and that might put minds at ease and lower prices. You shouldn't rule that possibility out. You're operating on incomplete information, and the outcome may surprise you. It's rational to consider and hedge for that possibility.
On the other hand, when I look at the Egyptian production curve, it looks like the global one, with OPEC oil shocks placed in the same locations on the time axis.
At the top level, URR = the sum of three variables
- cumulative production
- discovered reserves
- undiscovered resources
Going further, #2 is defined as- proved reserves, P > 90%
- probable reserves, P > 50%
- possible reserves, P in a low range, also known as P10, P20 reserves
I would define "discovery" as the sum of (undiscovered resources, possible or probable)So, when considering countries (oil provinces?) that may or may not give a good Hubbard Linearization "fit", it is prudent to ask whether they are candidates for a "noisy" discovery curve where discovery is as defined here. This will depend on various factors including how long they've been in production of any kind and how fully geologically vetted their resources have been -- their maturity as oil producers. The more mature an producing region is, the fewer discoveries (as defined here) I would expect, ie. there is less noise possible in the curve.
Finally, the historical UK and Texas in 1935-45 are "exceptions" because discoveries were not all in. Saudi Arabia is asserting that they are an exception -- some of us do not believe them. Some countries like Angola are not mature because they are in the early stages of production (offshore exploration continues) and new proven fields are just now in development.
On the "exception" thing - I think that what exacerbated the UK situation is that production was following so closely on the heels of discovery - there was much more separation in the US case - presumably because the industry was growing itself there, while in the UK case there was already a large hungry global oil industry ready to pounce on a new medium-sized province.
Re: the "exception" thing -- Time is the variable. The UK production curve was compressed in time, the US case was not. Historically, things have changed. In all future cases, it will look much more like the UK where production follows closely on discovery (however defined). After all, demand grows, we need more supply to meet that demand and in the end we have doubts about that supply because, afterall, this is the Peak Oil site :)
http://www.theoildrum.com/uploads/linearization.gif
and if you adjust to the currently accepted global cumulative, you get
http://img162.imageshack.us/img162/3029/cumprod1as.gif
The data looks more hyperbolic and the straight line part of the data is less pronounced. TOD had 1050 bbls and the current estimate is 950 bbls.
Is someone massaging the data to fit the logistic model? As I will continue to say: there is no need to do this, as you can stay intellectually honest if you just get away from the dang logistic model and use something that matches a simple physical process!
I'm getting the feeling you don't understand the basis for why the logistic model is a reasonable thing to do here. Have you read the Wikipedia?
I would be happy to know, given the uncertainties, what that "something" is.
http://mobjectivist.blogspot.com/2005/09/oil-shock-model.html
http://mobjectivist.blogspot.com/2005/09/oil-shock-model-continuous.html
http://mobjectivist.blogspot.com/2005/09/rc-circuit-analogy.html
I don't believe you or Stuart or me are in serious conflict about Peak Oil issues, I believe we're all on the same side.... we're arguing about details (that matter) but still, merely details....
best, Dave
- Claim is that an oil region (or other phenomenon) subject to (wannabe) exponential growth will produce in a sigmoid function.
- The derivative of a sigmoid can be graphed to make a clean straight line that shows (in this case) the total oil to be produced.
- Graphs of mature oil regions do tend to show the straight line.
- Therefore, they're probably sigmoids, and the graph can be used to deduce total production. (And with a bit more work, peak production rate and post-peak production decrease.)
So far, I'm with you. I plotted a sigmoid for the Saudi data, and it did in fact fit very closely to the linear data--not only in the slope, but in the number and spacing of data points.But to apply this method to nations and the world, you need to make a further assumption: that if you take the sum of several oil production baskets, you will still get a sigmoid.
In fact, the sum of sigmoids is not generally a sigmoid. The first paragraph of section III of http://hep.ucsb.edu/people/ascott/fermilab-conf-90-94.pdf (p. 6 or 7) implies that almost any function can be represented by a sum of sigmoids.
So to use this method for baskets of oil fields, you have to explain why in this case the sum of sigmoids is a sigmoid. I did a bit of Googling and couldn't find anything about the conditions that would make that true. If you have a power-law distribution, of course, you may have one or two oil fields dominating the curve--in which case you're calling all the rest "noise."
I could sort-of believe that the sum production of oil fields found in a single political and geographic area formed a sigmoid--though UK shows that even that isn't necessarily the case.
Perhaps we have to specify: sum production of oil fields found in a signle political and geographic area at approximately the same time. But then I find it very hard to believe that this method can be used for the world, and it must be used with care even on single nations.
Chris
Production rate (derivative of sigmoid) is a distribution, and maybe that's what you're talking about. So I guess you're saying that the production rate from a basket of oil (wells, fields, nations) is Gaussian.
Is the integral of a Gaussian a sigmoid? I couldn't find that on Google.
That's one of the features that Michael Lynch scoffs at when he looks at these models. He doesn't say it in exactly this way, but assuming gaussians in particular breaks causality. He extends this to sigmoids when he sees the long negative tail. While I don't agree with this completely, as you typically start the sigmoid at some finite value, no one has ever articulated where it should start.
In nature, when you use the logistic model, it starts with a small population of discrete entitities, and you let it proceed to (consume/infect/kill/bond) one entity. Then you can sit back and watch as the reaction propagates.
This problem reminds me of the non parametric density function estimation techniques used in statistics for the estimation of a probability density function from a limited set of observed random samples
where K() is the kernel function. In our case,(x_i, y_i):f(x)would be the country total production andx_i, y_i, h_iwould be the peak production date, peak production and depletion rate respectively for each oil field i. K() would be the normalized Hubbert function.kind of, it's called an erf function ( "error function").
I was going to ask whether Hubbert linearization will work on an "erf function" or not.
But before I ask that... it sounds like we can't expect the curves to add to a Gaussian anyway, since they're not a probability distribution.
So let me ask again the more direct question: Under what conditions is the sum of sigmoids a sigmoid? And, are these conditions approximated by oil-field baskets?
A Statistical Model for the Simulation of Oil Production
You can't add sigmoids directly (cumulative productions) because they are not temporally related (each field does not reach the same cumulative production at the same time). The right question is Under what conditions is the sum of sigmoid first derivatives a mono-peak function. From the simulation I made, it looks like it depends strongly on the shape of discovery distribution.
Your single-peak derivative criterion is too weak. The point of a sigmoid is that the "linearized graph" of its derivative produces a straight line that points at total production. For other shapes of derivative, even if they have a single peak, they won't produce that nice useful straight line.
And this makes me suspicious that linearized graphs of derivatives of baskets only produce straight lines accidentally or when one pulse of exploration dominates the basket. That would make "Hubbert linearization" not generally useful.
Chris
http://www.cut-the-knot.org/Curriculum/Algebra/LogisticModel.shtml
Scroll down to small values of P and R and you can see how touchy the whole thing is. Touchy too on initial conditions, which is always conveniently swept under the rug in these discussions.
Now, at 1980 the UK production is 1.8 Mb/d or 660 Mb/yr and the cumulative is 2100 Mb. So the annual is 31% of the cumulative. In 2004 we are back to about 660 Mb/yr on 21300 cumulative or 3%. The first big problem is that the curve doesn't really tend to linearize until the annual production is a small % of the cumulative production. At a fixed annual production it doesn't linearize then either, it just looks linear on the scale we are using. Saudi Arabia for example is producing about 3.5 Gb/yr on a cumulative 105 GB or a little over 3 %, so they look pretty linear.
If you just take a case where production is constant at 1 x/yr, for the first year production over cumulative is 100%, on the second year it is 50%, on the third year it is 33% etc, and you have to get out about 15 years and below 7% before the increments are small enough to start to look linear.If you are increasing production you will have a flatter slope depending on the rate of increase. It takes only a little effort to understand that to project URR you have to be past the peak and you have to have unconstrained production at the optimum rate that does not damage the field. If these 2 conditions are not met the projection will give a false URR. I suspect you have to also have something pretty close to a logistic curve, but I am not mathematician enough to explain that.
The UK curve is past the second peak now as of 1999 and is probably in irreversibla decline. The decline so far has been at an absolute rate of about 70 Mb/yr/yr, which on a 1999 production of 1070 Mb was 6.5% and in 2005, on a 2004 production of 730 Mb is 10%.
In the case of Saudi Arabia we have constrained production below the peak due to lack of world refinery capacity for their sour crude. As a first order approximation, if their production were declining at a rate of 50Mb/yr/yr they would show a URR of about 190 GB, essentially what we see. If production is constant at 3.5 Gb/yr the apparent URR would be about 240 Gb. If production were still growing at 50 Mb/yr/yr the apparent URR would be 320 Gb. This last would be the case if they can bring on enough new production to offset declines and if increasing world refinery capacity lets them sell an incremental 50 Mb/yr of sour crude each year until they get to annual production of near 4 Gb/yr or 11 Mb/d.
We saw some weeks ago that SA light sweet crude peaked somewhere between 2000 and 2004. If their light sweet crude is unconstrained and is declining at about 50 Mb/yr/yr, then the Laherrere URR projection may be valid for light sweet crude only, which to me seems like a pretty likely case. That could still leave their total URR more like 260 Gb without straining my credulity. My guess is that their present frantic efforts to increase drilling is precisely because their light sweet crude is in decline.
The last kicker comes in because I think that using maximum reservoir contact wells blows the whole Hubbert picture. It allows near peak production well beyond 50% depletion, but will almost surely result in a precipitous decline when the peak is passed. In the case of SA, when the water cut reaches the MRC wells, production will fall off a cliff. I think their MRC wells are pretty recent, and that they may have intentionally constrained production somewhat below the possible peak rate for these wells, so they may not have visibly distorted the curve yet.
I would expect the curve to begin moving to a less steep slope soon, and then after a few years get very steep, probably with an X intercept for light sweet crude pretty close to the Laherrere projection. Of course all this last bit is just speculation on my part. Murray
Oil Production in the Lower 48 States
Kaufmann & Cleveland, 2001
http://www.bu.edu/cees/people/faculty/cutler/articles/Oil_Prod_Lower_48.pdf
They use a modified Hubbert model, including political and economic factors to account for oil production behavior, including the decisions of the Texas Railroad Commission (analgous to OPEC on the world scale).
They conclude that Hubbert was very lucky - the factors which are most salient to the 1970 peak outcome were the non-geologic ones he had the least ability or information to predict, and which have no support in his model.
Any final conclusions?
As best that I can tell, there do not seem to be any counterexamples of regions showing--once they have established substantial oil production over period of 20 to 30 years--significant deviations from a downward linear slope.
My conclusion is that we all need to be looking into starting organic gardens and/or farms and moving to much smaller more energy efficient homes closer to where we work, preferably along mass transit lines.
Jeffrey J. Brown
As to what to do, I'm not sure I understand all the options well enough to have developed a solid position yet.
I ran across this paper a while back, and it may be useful to you. One thing to look at is the effect that excess production can have on a Deffeyes plot.
http://pages.ca.inter.net/~jhwalsh/deffeyesplot.pdf
In other words, if you would want to exclude political influences the thing you should not do is look at individual nations curves.
Obviously the Russian production increase in the last 10 years is mostly a result of the para-capitalist structures coming into place, so less related to prices. (It'll be fascinating to me see how rapidly Putin screws it up and provides attribution-error peak-oil fodder.)
Anyway, I'd love to see some of these production charts overlayed with prices.