When Does Hubbert Linearization Work?
Posted by Stuart Staniford on September 29, 2005 - 4:17am

Hubbert Linearization of Saudi Oil Production. Credit Jean Laherrere.
An interesting question is to know when does this style of Hubbert Linearization work? The empirical answer for a small non-random sample of five countries and one state is that it always seems to work as a pretty decent rough approximation once the graph has settled down into the linear regime. If anyone wants to post, or make, or suggest I make, a few more pictures, we can take this further. I would be particularly interested if anyone can come up with a country that has a decent section of linear regime that then goes substantially non-linear. The rest of the pictures are below the fold.
Romania

United States

Credit Seppo Korpela.
Iran

Norway
Credit Rune Likvern.
Texas

Credit Jeff Brown.

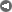


Thanks again Stuart for this kind of analysis.
I think TOD should create a special page with this information, explaining the linearization method, with these plots and the world plot Stu posted a couple of days ago with BP data.
Peak Oil is not a theory is a mathematical interpretation of Mother Nature.
For a producer following this strategy, the graph will take the non-linear form y=1/x, and foul up the linear extrapolation.
Also, has there ever been a case where the line actually hit the x-axis?
I'm still getting my head around these graphs, but isn't the slope telling you how fast they are depleting their reserve? Look at the Iran graph, very shallow slope compared to Norwegian. Doesn't this mean that extraction rate becomes ever smaller with respect to cumulative removed if extraction rate is held constant? Even a fixed rate of extraction for very long time will still have a negative slope estimating total reserve. Only increasing extraction rate keeps the slope positive.
If extraction rate peaks than the slope gets steeper. If I understand your post you say that SA is artificially holding production below their maximum rate. They could increase extraction rate and shift the slope into positive territory or so flat intersection with the X axis is meaningless? This is what the left side of all charts shows. Extraction rate is increasing faster than cumulative.
But I am skeptical that after decades of pumping SA can increase their rate enough to change the slope very much. This would imply that very few of their wells have peaked and many have the potential for increased rate of extraction. By increasing rates everywhere they could push the intersection to the X axis a bit to the right. But this short term effect could be corrected later by steeper declines in extraction rate than previously calculated during the push for maximum extraction rate.
Am I on the right track here or just completely lost mathmatically?
Oh, I forgot, asymptotes are features of junk science.
Seriously, it's like asking why log-log graph paper does not have any zero intercepts.
This too would lead to a y=1/x type curve.
Fossil Fuels Set to Become Relics, Says Research Group
Quote: "Energy markets are about to experience a seismic shift," Christopher Flavin, president of the Washington, D.C.-based Worldwatch Institute, said in a speech to oil executives and energy ministers in Johannesburg, South Africa, site of the 18th World Petroleum Congress. "The question for oil executives is whether you're in the oil business or the energy business."
The article paints a rosy picture of renewable energies, but one thing is clear: Peak oil awareness is entering the mainstream. We're still not being told the truth, tho, about the shock it'll mean for our society...
It is now their Most Popular Story (in terms of # of times e-mailed)
where D stands for the greek symbol Delta,
Dk/kandDQ/Qare the relative errors on k and Q which can be presumed constant. The error behaves has following:- Production start Q -> 0:
- Production Q -> 1 (total URR has been extracted):
Because we are in log domain,D(ln(aP/Q)) = -infinitymeans that deviation around the asymptotic line will tend toward zero! That's why, we observe these wild deviations aroud the line when production is starting whereas it seems to converge nicely when Q tend toward 1. This behavior can be misleading for an observer because it seems to reinforce that there is some inexorable mechanism at work pushing the production data around the line.Hubbert was not a mathematician or an econmist. He drew his curves by hand, and calculated the areas underneath them by counting the squares on his graph paper and guessing. He assumes logistic growth and decline, and some of the field curves look like logistic curves.
But I'm not seeing a lot of advanced statistical (or econometric) methods or models yet from the peakers. Drawing and fitting curves is meaningless - its the equations the curves reflect and the relation of the variables in the equations to the facts in the ground that provide meaning.
If this non-argument is the best you can do, maybe the Peak Oil people are right.
Let's try to imagine under what conditions this might happen. Once P/Q over Q goes linear for a while for some country, it can only go non-linear (upwards) depending on the maturity of the country's production, where I'll define maturity as "% of URR in production". Maturity is obviously fuzzy. There are basically two cases:
- maturity is high (some % = N1). The linear regime can not change much.
- maturity is low (some % = N2). What can happen? The country ramps up production on some undeveloped big fields they've got laying around. But bringing new fields online happens gradually, production starts low and rises thereafter until the peak for each field. Meanwhile, suppose existing fields are depleting. All you can get is a "Prudhoe Bay" kind of bump as shown in the US graph (depending on N2). In the best case, existing fields are not declining yet, N2 is fairly low and some new big fields are being brought online at the same time. In this case, you could go non-linear for some amount of time but on the other hand, the country has not settled into the linear regime for very long either.
I am confident that there is no country in the real world meeting the conditions for the Hubbert Linearization to go non-linear as outlined in #2 above. It's more complicated than my simple description but I think the basic intuition is right.Thus saving the world and reasserting their premier position of control among the world's oil producers. And don't forget, we love the Saudi Oil Minister Ali Al-Naimi. It's all good.
First, what are some sources for the raw production data for states and countries? I'd like to try making some of these curves myself.
Second, what does the curve look like for the whole world, at present? Is the recent data on a line?
Third, is there a name for these kinds of curves? They would be helpful to look up references where they are discussed, particularly in the context of oil extraction.
Here is one reference which is skeptical about these curves, from Michael Lynch, http://www.gasresources.net/Lynch(Hubbert-Deffeyes).htm. His figures 4 and 5 show production curves for fields which don't fall into this nice pattern. He analyzed all of the UK's top producing fields and of the top 21, only 7 showed nice curves like those above.
My main problem with the curves is that the theory behind them is unsound. There is no reason to expect oil production to match a logistic or "yeast growth" curve. The fact that empirically it has done so for some oil fields in the past cannot be validly extrapolated forward into the future because conditions will be so different.
In the past, when one field was dry they would move onto the next. But in the future, as each field dies it means there will be that much less oil supply in the world. The price will rise and people will work much harder to draw oil from existing fields. This additional motivation and effort, which was not present in the past, will move production above the previous linear regime and create a departure from the predicted curve.
Because of this effect I can predict with high confidence that we will eventually extract more oil from these fields than the graphs above predict. It is impossible however to say how much more we will get.
The lower the pressure, the lower the cost of making and fabricating the steel components for the synfuel plant. Oil well drilling will fall like a rock at some price and only the existing wells will continue to produce at a constantly decreasing rate.
Lynch's point about URR is that URR is partially an economic assessment of the ultimate amount of oil that will be recovered, similar to "proven reserves". Whereas "proven reserves" are the amount of OOIP that is economically recoverable under present economic and technological conditions, URR is an estimate of total future recovery based on projected economic and technological conditions. Even if we can only get 35% of the oil today, we might estimate that ultimate recovery rates will be 50%. Lynch argues that over time estimates of ultimate recovery rates have risen, thus raising URR.
As prices rise higher then we previously thought they'd go, and as technology improves faster than we previously thought it could, projected future final recovery rates rise. That implies URR should continue to increase relative to OOIP.
Dr. Tanstaafl --- aka "Silent E"
There Aint No Such Thing As A Free Lunch
I think this is the crux of what separates "peakoilers" and cornucopians. It's obvious that the URR will grow according to the current/technological conditions. However, it cannot grow forever and will reach an asymptote (75%-80% of the OOIP?). The application of enhanced oil recovery methods is also highly dependent on a particular oil field history/features and cannot be generalized across all fields. The need for new extraction methods reinforce the fact that oil is getting harder to get and more economically expensive which is exactly the point of "peakoilers".
His point is that Campbell's own numbers indicated URR rose over that 5 year period. That's where Lynch got the data for the chart! But Campbell never makes an effort to explain why the factors that drove reserve increases won't operate over the next 15 years as well, raising URR once again.
Another Way of Looking at CERA
Depletion theory
It gives the following fit (k= 0.0312, n=5.5635e-006, URR= 309 Gb):
picture
The maximum production rate is given by:
which gives 3.55 Gb (9.7 mbpd).
PDF at:
http://www.bu.edu/cees/people/faculty/cutler/articles/Oil_Prod_Lower_48.pdf
clearly, clear as i dont know what, SA is in decline and this should be published on every newspapaer, frontpage on every news website.
picture
you can see that you can estimate a second logistic line which gives an URR near 570 Gb.
Also, they seem to be creating more confusion than benefit. A negative slope does not mean that production is necessarily in decline, as Khebab earlier pointed out.
One more observation - as production declines for a country, unless it completely stops, it will never reach the x-axis. However, it also won't reach an asymptote. Instead, datapoints will cluster closer and closer together, nearing the x-axis but never making it there.
OPEC, however, has until recently been quota limited. With over capacity due in part to large non-OPEC production increases, the ME made little attempt to further develop its reserves after around the mid-eighties, and certainly not at a maximum clip. Indeed, their existing output could not be utilized. Accordingly, and because they followed their own economic rules, their curve is likely to be different from other countries. Consider Russia, with an earlier peak, followed by a decline, and then climbing to a new peak under a different political and economic environment.
Most have been surprised by the sharply growing Asian demand over the past few years. SA and others are only now responding to the high prices by looking to increase production. This effort is helped by their substantial increase in income, without which they would have anyway been unable to fund the effort. Simmons may be right that increased production will damage the fields, but it seems likely that production will nevertheless increase for a time.
The statement that the world peaks when SA peaks is not obviously correct. Increases in SA production, if realized, may offset worldwide decline, or perhaps not. And, future Siberian output, and its timing,is also murky.
In the real world, I think that the approach works because after decades of drilling in a given region--Texas; Saudi Arabia and now the world--there aren't many surprises left.
Here in Texas, the method predicted the peak of production (in 1972) within two years (assuming that peak production is at 50% of Qt). Texas peaked at 54% of Qt. Saudi Arabia is currently at 55%.
Another interesting analogy. The method gives Texas recoverable reserves of 66 billion barrels (Gb), and the method gives Saudi Arabia 180 Gb. Peak production in Texas was 3.5 MMBOPD. If you divide 180 by 66 and multiply times 3.5, you get: 9.5 MMBOPD, which is precisely what the EIA currently estimates as the Saudi's oil production. (By the way, note that 180 Gb is almost exactly the number that Matt Simmons cited as Saudi Aramco's estimate of recoverable reserves in 1970's).
There are other good analogies. The largest oil field in Texas, and in the Lower 48, is (or was) the East Texas Field. The first production peak in the East Texas field was in the Thirties, before the Texas RRC curtailed production. The final peak was in 1972--exactly when overall Texas oil production peaked. The East Texas Field is to Texas as the Ghawar Field is to Saudi Arabia.
We have had roughly 70 years of regulated oil production. From about 1935 to 1970, Texas served as swing producer. From about 1970 to 2005, Saudi Arabia served as swing producer. There is no longer a swing producer.
The production history in the 10 years after the Texas peak also serves as a cautionary model for the next 10 years. In the years following 1972, oil prices in nominal terms went up by 1,000%; the state saw the biggest drilling boom that we will ever see and the number of producing wells went up by 14% in the 10 years following 1972. It made no difference. Texas production declined by about 30% in the 10 years following the peak. We are currently down by almost 75%, 33 years after the peak.
By the way, based on some estimates I have made, since Katrina hit the world has used--from fossil fuel + nuclear sources--the energy equivalent of the entire recoverable reserves of the East Texas Field, about 6 Gb of oil. We use about one Gb equivalent every five days.
Jeffrey J. Brown
I am wondering what Brazil, Angola and Nigeria would look like. In the short-term (up to 2013 or so), they might go non-linear but since most of the new stuff is from deep-sea drilling, there would be a steep drop-off afterwards.
Michael Lynch's assumptions about new supply as a function of price & technology were discussed above. This reminds me of a slippery slope. I'll explain. From the wiki page:The connection between A and B is an historical one, so this looks like an induction (eg. the sun has always risen in the morning, therefore it will rise tomorrow). Everytime A has occurred historically, B inevitably follows. This is the article of faith.
However, the reasoning is flawed because conditions have changed, specifically
- Each time B occurs, more easily recoverable oil has been extracted and such (conventional) oil is ultimately limited by geology.
- Each time B occurs (ie. each time you go to the well, so to speak), you need more oil to make the resource plentiful with respect to demand than you did last time (eg. demand has never been at 84/mbd -- obviously demand can go down, but not much, certainly not to previous historical levels like 1982, the last time we faced this problem).
Now, the simple conclusion is that, from an historical perspective, the world has changed. Previous draws on oil and higher demand figures have changed it. You can not infer that Michael Lynch's B dynamic is always going to work. He thinks oil will never peak (or at least for a real long time). But there are limits to growth. As Dr. Tanstaafl --- aka "Silent E" said, there's no free lunch. Lynch seems to think that there is a free (actually low cost) lunch into indefinite future. I've got to disagree.Lynch is on the record stating that peak oil will happen after 2025 -- which is comparable to the forecasts of many other commentators (Total, Exxon/Mobil, IEA, EIA, BP, Laherrere).
There is no one who claims that oil will never peak. The idea that there are such people is a straw man, and it baffles me why peak oilers keep talking about these dissenters who do not believe in peak oil. I challenge you to produce even one person who seriously claims that oil will never peak.
What Lynch actually says in the referenced article is:
Clearly, what Lynch is saying is that no imminent peak in non-OPEC oil (or global oil) was in sight at the time the article was written, not that there will be no visible global peak.
http://www.cera.com/news/details/print/1,2317,7453,00.html
This is an admission of peak oil. The peak will be a long plateau, lasting several decades, but it will definitely end.
Like I said, no one believes peak oil will not occur, not even the most extreme optimists. The person who "doesn't believe in peak oil" is a myth, like the unicorn.
Two years ago NO-ONE of the energy companies and institutions, and much less economic institutes believed in or spoke about Peak Oil. Only in the last year, as it has become evident that supply is not infinite, are analysis starting to accept there will be one. And only in the last months do some economist abandon the flat-earth belief. But, I'm sorry to say, predicting a peak in 2035 and then a decade-long plateau is nearly as much as saying there won't be one.
If 2005/6 is the PO year, in 2010 everyone will make predictions with a peak in 2005/6, and you will probably kindly point to us all the studies that, o wonders of wonders, admit the peak. In the USA of the late 70s, you would probably have said that nobody thought that Hubert was wrong.
Please, stop making that kind of inflammatory comments, and stop only answering to the questions easy to attack, and ignoring the ones that debunk you.
Mike, if you can supply even one quote from someone who seriously claims the supply of oil is infinite, I will grant your point.
EIA oil supply forecast from 2004: http://www.hubbertpeak.com/us/eia/oilsupply2004.htm
Scroll down to see figure 2. Yes, they finally recognise Peak Oil, but I repeat, saying that the expected PO year is 2037 is like saying: yes, production will peak... sometime in the far, far future. So we have half a century of slightly more expensive oil. Completely ridiculous.
I could go on and on, but as of September 2005, it is not so easy anymore to find flat-earth statements as it was just a few months ago (somebody knows more blatant flat-earth statements please help with this stupid argument).
And hell, if you had said: "In the course of the last few months, on the face of rising oil prices, and the supply problem becomming evident, nearly everyone has at last acknowledged that there will be an Oil peak", then I wouldn't have said anything. But your statement was simply not true, and you should know it. I see it already comming, a few years after PO, everybody will be saying: "But we never ever said oil production will grow forever". And after their ridiculous 2020+ PO dates (they only adopted after about the year 2000) have been proven false, they will point at their past years forecast (witch of course will have been made after PO happened) and say "you see, we are in decline, like we said".
That's a question. He's not making a commitment one way or the other. He's said "it's fair to ask", not "here's the answer".
It's also taken out of context:
http://www.chevron.com/news/archive/chevron_speech/1999/1999-11-30.asp
Why would it be logical to worry about decline and depletion if oil is infinite and will never peak?
The "Geopolitics and Energy" forecast numbers are from the IEA. Oddly enough, their figure for 2005 is too low. They predicted 82mbd, and it's closer to 84.
The IEA admits that oil is finite and will peak:
http://www.peakoil.net/uhdsg/weo2004/TheUppsalaCode.html
As you note, the EIA recognizes peak oil, and thus is obviously not stating that oil supplies are infinite.
I could go on and on,
Yes, but you're just spinning your tires. You're not producing anyone who believes the supply of oil is infinite and will never peak. I'm telling you, no matter how far back you go, you will never find a person who seriously claimed that the supplies of oil located in the crust of the earth are infinite, and that oil production will continue growing forever in an exponential fashion. There is no such person. Anyone who puts 5 minutes of thought into it knows that oil is finite, and therefore must eventually peak. People just had it on the back burner for a while because they didn't believe it was close enough to worry about. Putting peak oil on low priority is a completely different thing from explicitly stating that it will never occur.
But your statement was simply not true, and you should know it.
You haven't refuted it yet. You still haven't produced even one person who says crude oil will never peak. That's because there is no such person. Please, think about it. The earth is finite. Therefore any material good produced from it must eventually peak. It's not rocket science. Everyone understands that, and always has. The only person you will find to disagree with that is someone who is mentally defective.
a few years after PO, everybody will be saying: "But we never ever said oil production will grow forever"
Yes, and they will be completely correct in saying that because no one ever did say oil production will grow forever. If you disagree, please dig harder and find one person who said: "oil production will grow forever".
And after their ridiculous 2020+ PO dates (they only adopted after about the year 2000) have been proven false,
Colin Campbell's PO dates have been proven false on two or three occasions and it didn't affect his credibility.
http://sepwww.stanford.edu/sep/jon/world-oil.dir/lynch/figure3.gif
And we don't know how far off he is yet. You seem to be convinced that we are peaking right now (or will peak next year), but that is just a prediction, not a fact.
Anyway, only time will tell.
"Then there is the oil we that we might produce, not from fossils, but from new crops--palm oil, soybean oil, and so on. Clearly, there is no meaninful limit to this source excep the sun's energy (land and water are not limits -- see chapters 6 and 10). The notion of finiteness is making ever less sense as we proceed)."
And "After our sun runs out of energy, there may be nuclear fusion, or some other suns to take care of our needs. We've got seven billion years to discover solutions to the theoretical problems that we have only been able to cook up in the past few centuries of progress in physics. It's reasonable to expect the supply of energy to continue becoming more available and less scarce, forever."
Professor Simon was a professor of Business Administration at the University of Maryland. The book quoted above was published by a major university press (Princeton), and thus presumably peer-reviewed.
You might have me there, Stuart, but I'd have to see the context to be sure. We've already seen a couple of cases of selective quoting on this tangent. What's Simon's rationale for saying that oil is nonfinite?
As for energy, I agree with Simon. I personally believe the human destiny is to intensively harvest the energy of the sun using space power satellites, space mirrors and other forms of space solar power. That's a lot of energy out there, and when we get done with that there is a whole universe humming with massive power flows. This has nothing to do with oil, however. Peak oil and peak energy are two different things. Peak oil is inevitable, peak energy isn't.
Simon's comments on vegetable oils are perfectly correct. There is no meaningful limit on the cumulative volume of those oils produced.
The rest of his comments pertain to energy, not oil, and thus are irrelevant to the challenge of producing a person who believes oil will never peak.
Source
The following link ("Why are launch costs so high") is detailed and interesting:
http://www.ghg.net/redflame/launch.htm
This has the asymptotic property of "appearing" to intercept the Y-axis at zero. However, it never gets there. The behavior is correct, but it has nothing to do with the logistics function. It's more like a very thin man walking toward a wall, every second going halfway there, and then realizing mathematically that he will never hit the wall.
And then notice how the curves match best when we are deep into depletion (i.e. Texas). At that point, there is really no use figuring out URR; to use an electronics analogy, we are just discharging the capacitor in an RC circuit.
Good stuff, but as you know, I like to get the maximum insight out of the model that I can.
What I find fascinating about his position is that he is saying that while individual (nonrenewable) sources of energy will peak and then decline, our overall supply of nonrenewable energy--which is after all the sum of individual sources--will never decline.
This is exactly analogous to saying that while individual oil wells in a field will peak and decline, but the overall production from the field--which is the sum of the production from individuals wells--will never decline.
In regard to conventional versus non-conventional oil production, the history of Texas gas production again offers a cautionary lesson. Texas gas production peaked about the same time as oil. Gas production has not declined as much as oil, partly because of non-conventional sources such as shale gas. However, we are still significantly below our peak gas production level in the Seventies. In other words, non-conventional gas only served to slow the rate of decline of total gas production.
In my opinion, we will see the same pattern regarding oil, i.e., non-conventional oil production will only serve to slow the rate of decline of total oil production. By the way, according to the EIA, total Canadian oil production is down year over year. In other words, tar sands production is not even keeping up with the decline in conventional Canadian oil production--let alone doing anything to offset declines elsewhere.
Jeffrey J. Brown
For me the million dollar question is:
How does the peak year predicted by these analyses compare to the actual peak year for each of these countries? This does not seem to be addressed here.
It would certainly help, to give some insight as to the likely accuracy of current predictions for the world peak using this method, by yourself, Deffeyes and others.
Jeffrey J. Brown